题目内容
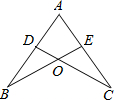
如图，已知AB=AC，∠1=∠2，∠B=∠C，则BD=CE．请说明理由：
解：∵∠1=∠2
∴∠1+∠BAC=∠2+______．
即∠EAC=∠DAB．
在△ABD和△ACE中，
∠B=______（已知）
∵AB=______（已知）
∠EAC=______（已证）
∴△ABD≌△ACE（______）
∴BD=CE（______）
解：∵∠1=∠2
∴∠1+∠BAC=∠2+______．
即∠EAC=∠DAB．
在△ABD和△ACE中，
∠B=______（已知）
∵AB=______（已知）
∠EAC=______（已证）
∴△ABD≌△ACE（______）
∴BD=CE（______）
∵∠1=∠2，
∴∠1+∠BAC=∠2+∠BAC，
即∠EAC=∠DAB，
在△ABD和△ACE中，
∠B=∠C（已知），
∵AB=AC（已知），
∠EAC=∠DAB（已证），
∴△ABD≌△ACE（ ASA），
∴BD=CE（全等三角形的对应边相等）．
故答案为：∠BAC，∠C，AC，∠DAB，ASA，全等三角形的对应边相等．
∴∠1+∠BAC=∠2+∠BAC，
即∠EAC=∠DAB，
在△ABD和△ACE中，
∠B=∠C（已知），
∵AB=AC（已知），
∠EAC=∠DAB（已证），
∴△ABD≌△ACE（ ASA），
∴BD=CE（全等三角形的对应边相等）．
故答案为：∠BAC，∠C，AC，∠DAB，ASA，全等三角形的对应边相等．
练习册系列答案
阅读快车系列答案
相关题目
