题目内容
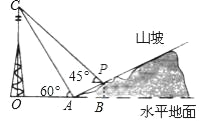
【题目】如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度=1:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置P的铅直高度PB.(测倾器高度忽略不计,结果保留根号形式)
【答案】![]() 米
米
【解析】分析:如下图,过点P作PF⊥CO于点F,在Rt△AOC中由已知易得OC=![]() ,设PB=x,则由已知可得AB=2x,OF=PB=x,由此即可得到PF=OB=100+2x,CF=OC-OF=
,设PB=x,则由已知可得AB=2x,OF=PB=x,由此即可得到PF=OB=100+2x,CF=OC-OF=![]() ,由Rt△CPF中,∠CPF=45°可得PF=CF,从而可得
,由Rt△CPF中,∠CPF=45°可得PF=CF,从而可得![]() ,解此方程即可求得PB的值.
,解此方程即可求得PB的值.
详解:
作PE⊥OB于点E,过点P作PF⊥OC,垂足为F.
在Rt△OAC中,由∠OAC=60°,OA=100,得OC=OAtan∠OAC=![]() (米),
(米),
过点P作PB⊥OA,垂足为B.
由i=1:2,设PB=x,则AB=2x.
∴PF=OB=100+2x,CF=![]() ﹣x.
﹣x.
在Rt△PCF中,由∠CPF=45°,
∴PF=CF,即100+2x=![]() ﹣x,
﹣x,
∴x=![]() ,即PB=
,即PB=![]() 米.
米.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目