Question

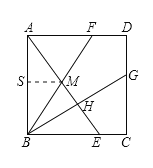
【题目】正方形ABCD的边长为4，E为BC边上一点，BE=3，M为线段AE上一点，射线BM交正方形的一边于点F，且BF=AE,则BM的长为____．

Answer 1

【答案】或

【解析】

分两种情况进行分析，①当BF如图位置时，②当BF为BG位置时；根据相似三角形的性质即可求得BM的长．

如图，当BF如图位置时，

∵AB=AB，∠BAF=∠ABE=90°，AE=BF，
∴△ABE≌△BAF（HL），
∴∠ABM=∠BAM，
∴AM=BM，AF=BE=3，
∵AB=4，BE=3，
∴AE= ，
过点M作MS⊥AB，由等腰三角形的性质知，点S是AB的中点，BS=2，SM是△ABE的中位线，
∴BM=AE=×5=，
当BF为BG位置时，易得Rt△BCG≌Rt△ABE，
∴BG=AE=5，∠AEB=∠BGC，
∴△BHE∽△BCG，
∴BH：BC=BE：BG，
∴BH=．

故答案是：或．