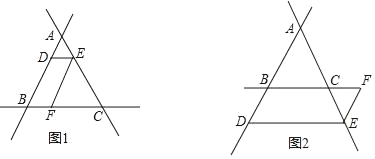题目内容
【题目】如图,在△AOB中,OA=OB,∠AOB=50°,将△AOB绕O点顺时针旋转30°,得到△COD,OC交AB于点F,CD分别交AB、OB于点E、H.求证:EF=EH. 
【答案】证明:∵OA=OB,∠AOB=50°, ∴∠A=∠B.
∵将△AOB绕O点顺时针旋转30°,得到△COD,
∴∠AOC=∠BOD=30°,OD=OB=OA,∠D=∠B.
在△AOF和△DOH中,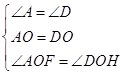 ,
,
∴△AOF≌△DOH(ASA),
∴OF=OH,
∵OC=OB,
∴FC=BH.
在△FCE和△HBE中, ,
,
∴△FCE≌△HBE(AAS),
∴EF=EH.
【解析】根据等腰三角形的性质,可得∠A与∠B,根据旋转的性质,可得∠AOC=∠BOD=30°,OD=OB=OA,∠D=∠B,根据全等三角形的判定与性质,可得答案.
【考点精析】利用旋转的性质对题目进行判断即可得到答案,需要熟知①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
【题目】两会期间,记者随机抽取参会的部分代表,对他们某天发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,请结合图中相关数据回答下列问题:
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
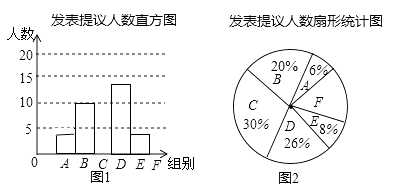
(1)求得样本容量为 , 并补全直方图;
(2)如果会议期间组织1700名代表参会,请估计在这一天里发言次数不少于12次的人数;
(3)已知A组发表提议的代表中恰有1为女士,E组发表提议的代表中只有2位男士,现从A组与E组中分别抽一位代表写报告,请用列表法或画树状图的方法,求所抽的两位代表恰好都是男士的概率.