题目内容
【题目】将推理过程填写完整
如图，EF∥AD，∠1 =∠2，∠BAC = 70°。求∠AGD的度数。
解：因为EF∥AD（已知）
所以 ∠2 = （两直线平行，同位角相等）
又因为 ∠1 = ∠2（已知）
所以 ∠1 = ∠3（等量代换）
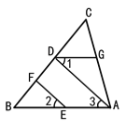
所以AB∥ （ ）
所以∠BAC + = 180°（ ）
又因为∠BAC = 70°（已知）
所以∠AGD =
【答案】见解析.
【解析】
根据平行线性质推出∠2=∠3，根据平行线判定推出AB∥DG，根据平行线判定推出∠BAC+∠AGD=180°，求出即可．
因为EF∥AD(已知)，
所以 ∠2 =∠3(两直线平行，同位角相等)，
又因为 ∠1 = ∠2(已知)，
所以 ∠1 = ∠3(等量代换)，
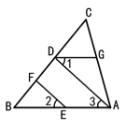
所以AB∥DG(内错角相等，两直线平行)，
所以∠BAC + ∠AGD = 180°(两直线平行，同旁内角互补)，
又因为∠BAC = 70°(已知)，
所以∠AGD =110°，
故答案为：∠3；DG；内错角相等，两直线平行；∠AGD；两直线平行，同旁内角互补；110°.
练习册系列答案
阅读快车系列答案
相关题目
