题目内容
【题目】(问题情境)
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(探究展示)
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
(拓展延伸)
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.

【答案】(1)证明见解析;(2)AM=DE+BM成立,证明见解析;(3)①结论AM=AD+MC仍然成立;②结论AM=DE+BM不成立.
【解析】
(1)从平行线和中点这两个条件出发,延长AE、BC交于点N,易证△ADE≌△NCE,得到AD=CN,再证明AM=NM即可;(2)过点A作AF⊥AE,交CB的延长线于点F,
易证△ABF≌△ADE,从而证明AM=FM,即可得证;(3)AM=DE+BM需要四边形ABCD是正方形,故不成立,AM=AD+MC仍然成立.
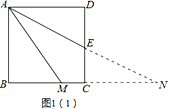
(1)延长AE、BC交于点N,如图1(1),
∵四边形ABCD是正方形,∴AD∥BC.∴∠DAE=∠ENC.
∵AE平分∠DAM,∴∠DAE=∠MAE.∴∠ENC=∠MAE.∴MA=MN.
在△ADE和△NCE中,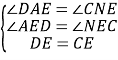
∴△ADE≌△NCE(AAS).∴AD=NC.∴MA=MN=NC+MC=AD+MC.
(2)AM=DE+BM成立.
证明:过点A作AF⊥AE,交CB的延长线于点F,如图1(2)所示.
∵四边形ABCD是正方形,∴∠BAD=∠D=∠ABC=90°,AB=AD,AB∥DC.
∵AF⊥AE,∴∠FAE=90°.∴∠FAB=90°﹣∠BAE=∠DAE.
在△ABF和△ADE中,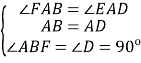
∴△ABF≌△ADE(ASA).
∴BF=DE,∠F=∠AED.
∵AB∥DC,
∴∠AED=∠BAE.
∵∠FAB=∠EAD=∠EAM,
∴∠AED=∠BAE=∠BAM+∠EAM=∠BAM+∠FAB=∠FAM.
∴∠F=∠FAM.
∴AM=FM.
∴AM=FB+BM=DE+BM.
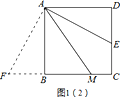
(3)①结论AM=AD+MC仍然成立.②结论AM=DE+BM不成立.

【题目】在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色的球20只,某学习小组做摸球实验.将球搅匀后从中随机摸出一个球,记下颜色,再把它放回袋中,不断重复,下表是活动进行中记下的一组数据
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请你估计,当n很大时,摸到白球的频率将会接近 (精确到0.1).
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 .
(3)试估算口袋中黑、白两种颜色的球有多少只.

