题目内容
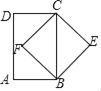
【题目】已知:如图,菱形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,且BE=BF=DH=DG.
(1)求证:四边形EFGH是矩形;
(2)已知∠B=60°,AB=6.
请从A,B两题中任选一题作答,我选择 题.
A题:当点E是AB的中点时,矩形EFGH的面积是 .
B题:当BE= 时,矩形EFGH的面积是8![]() .
.

【答案】(1)证明见解析;(2)A或B;A题:9![]() ;B题:2或4.
;B题:2或4.
【解析】
(1)根据题意与菱形的性质证得∠AEH+∠BEF=![]() (180°﹣∠A)+
(180°﹣∠A)+![]() (180°﹣∠B)=90°,同法可证:∠EFG=∠EHG=90°,根据矩形的判定即可得证;
(180°﹣∠B)=90°,同法可证:∠EFG=∠EHG=90°,根据矩形的判定即可得证;
(2)A题:连接AC,BD交于点O.根据题意与菱形的性质可得△ABC是等边三角形,根据等边三角形的性质可得个边长的长度,然后根据矩形的面积公式求解即可;
B题:设BE=x,则AE=6﹣x,EF=x,EH=![]() (6﹣x),根据题意可列出关于x的方程,然后解方程即可.
(6﹣x),根据题意可列出关于x的方程,然后解方程即可.
(1)证明:∵四边形ABCD是菱形,
∴AD∥BC,AB=BC=CD=AD,
∴∠A+∠B=180°,
∵BE=BF=DH=DG,
∴AE=AH=CF=CG,
∴∠AEH=∠AHE=![]() (180°﹣∠A),∠BEF=∠BFE=
(180°﹣∠A),∠BEF=∠BFE=![]() (180°﹣∠B),
(180°﹣∠B),
∴∠AEH+∠BEF=![]() (180°﹣∠A)+
(180°﹣∠A)+![]() (180°﹣∠B)=90°,
(180°﹣∠B)=90°,
同法可证:∠EFG=∠EHG=90°,
∴四边形EFGH是矩形;
(2)解:A题:连接AC,BD交于点O.
∵AE=BE,
∴AH=DH,BF=CF,CG=GD,
∴EF=![]() AC,EH=
AC,EH=![]() BD,
BD,
∵AB=BC=6,∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=6,
∵OB⊥AC,
∴OB=3![]() ,BD=2OB=6
,BD=2OB=6![]() ,
,
∴EF=3,EH=3![]() ,
,
∴S矩形EFGH=EFEH=9![]() .
.
故答案为9![]() ;
;
B题:设BE=x,则AE=6﹣x,EF=x,EH=![]() (6﹣x),
(6﹣x),
由题意:x![]() (6﹣x)=8
(6﹣x)=8![]() ,
,
解得x=4或2,
∴BE=2或4.

 名校课堂系列答案
名校课堂系列答案