题目内容
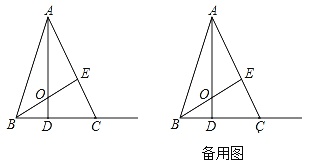
【题目】如图,在□ABCD中,对角线AC,BD交于点O,过点O作EO⊥BD,交BA延长线于点E,交AD于点F,若EF=OF,∠CBD=30°,BD=![]() .求AF的长.
.求AF的长.

【答案】2
【解析】试题分析:方法一,由平行四边形的性质得OD=![]() ,解Rt△ODF,求出OF和FD的长. 过O作OG∥AB,交AD于点G,易证△AEF∽△GOF,从而得到AF=GF.然后根据
,解Rt△ODF,求出OF和FD的长. 过O作OG∥AB,交AD于点G,易证△AEF∽△GOF,从而得到AF=GF.然后根据![]() 列方程求解.
列方程求解.
方法二,由△ODF≌△OHB可知,OH=OF,从而得到![]() ,再由△EAF∽△EBH可得
,再由△EAF∽△EBH可得![]() ;解直角三角形Rt△BOH,求出BH的长,代入比例式求出AF的长.
;解直角三角形Rt△BOH,求出BH的长,代入比例式求出AF的长.
解:方法一:
∵□ABCD,∴AD∥BC,OD=![]() BD=
BD=![]() .
.
∵∠CBD=30°,∴∠ADB=30°.
∵EO⊥BD于O,∴∠DOF=90°.
在Rt△ODF中,tan30°=![]() ,∴OF=3.∴FD=6.
,∴OF=3.∴FD=6.

过O作OG∥AB,交AD于点G,∴△AEF∽△GOF,∴ ![]() .
.
∵EF=OF,∴AF=GF.
∵O是BD中点,∴G是AD中点.
设AF=GF=x,则AD=6+x,∴AG= ![]() .
.
解得x=2,∴AF=2.

方法二:延长EF交BC于H.
由△ODF≌△OHB可知,OH=OF.
∵AD∥BC,∴△EAF∽△EBH,∴ ![]() .
.
∵EF=OF,∴ ![]() .
.
由方法一的方法,可求BH=6,∴AF=2.

练习册系列答案
相关题目