题目内容
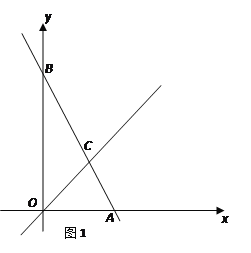
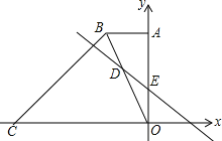
【题目】如图,在平面直角坐标中,直角梯形OABC的边OC、OA分别在x轴、y轴上,AB∥OC,∠AOC=90°,∠BCO=45°,BC=12![]() ,点C的坐标为(-18,0).
,点C的坐标为(-18,0).
(1)求点B的坐标;
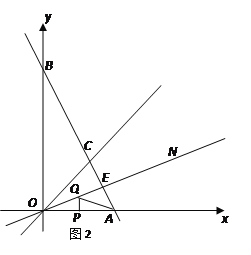
(2)若直线DE交梯形对角线BO于点D,交y轴于点E,且OE=4,∠OFE=45°,求直线DE的解析式;
(3)求点D的坐标.
【答案】(1)(-6,12);(2)y=-x+4;(3)D(-4,8)
【解析】
(1)过B作BG⊥x轴,交x轴于点G,由题意得到三角形BCG为等腰直角三角形,根据BC的长求出CG与BG的长,根据OC-CG求出OG的长,确定出B坐标即可;
(2)由题意得到三角形EOF为等腰直角三角形,确定出E与F的坐标,设直线DE解析式为y=kx+b,把E与F代入求出k与b的值,确定出直线DE解析式;
(3)设直线OB解析式为y=mx,把B坐标代入求出m的值,确定出OB解析式,与直线DE解析式联立求出D坐标即可.

解:(1)过B作BG⊥x轴,交x轴于点G,
在Rt△BCG中,∠BCO=45°,BC=12![]() ,
,
∴BG=CG=12,
∵C(﹣18,0),即OC=18,
∴OG=OC-CG=18-12=6,
则B=(﹣6,12);
(2)∵∠EOF=90°,∠OFE=45°,
∴△OEF为等腰直角三角形,
∴OE=OF=4,即E(0,4),F(4,0),
设直线DE解析式为y=kx+b,
把E与F坐标代入得:![]() ,
,
解得:k=﹣1,b=4,
∴直线DE解析式为y=﹣x+4;
(3)设直线OB解析式为y=mx,把B(-6,12)代入得:m=﹣2,
∴直线OB解析式为y=﹣2x,
联立得:![]() ,
,
解得:![]() ,
,
则D(﹣4,8).

 长江作业本同步练习册系列答案
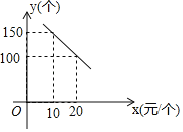
长江作业本同步练习册系列答案【题目】某经销商从市场得知如下信息:
某品牌空调扇 | 某品牌电风扇 | |
进价(元/台) | 700 | 100 |
售价(元/台) | 900 | 160 |
他现有40000元资金可用来一次性购进该品牌空调扇和电风扇共100台,设该经销商购进空调扇![]() 台,空调扇和电风扇全部销售完后获得利润为
台,空调扇和电风扇全部销售完后获得利润为![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)利用函数性质,说明该经销商如何进货可获利最大?最大利润是多少元?