��Ŀ����
����Ŀ���ۺ���ʵ��
�����龳���������۵��е���ѧ
��֪������ֽƬABCD�У�AB=4����E��AB���ϵ�һ�㣬��G��CE���е㣬��������ֽƬ��CE����ֱ���۵�����B�Ķ�Ӧ��Ϊ��B�䣮
(1)��ͼ1������BCE=30��ʱ������BG��B��G����֤���ı���BEB��G�����Σ�
����̽����
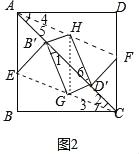
(2)��CD����ȡ��F��ʹDF=BE����H��AF���е㣬�ٽ�������ֽƬABCD��AF����ֱ���۵�����D�Ķ�Ӧ��ΪD����˳������B�䣬G��D�䣬H��B'���õ��ı���B��GD��H��
�����A��B��������ѡһ��������ѡ���� ���⣮
A�⣺��ͼ2������B'��D�������ڶԽ���AC��ʱ��
���ж�B��G��D��H��������ϵ��λ�ù�ϵ����˵�����ɣ�
��ֱд����ʱ��H��G֮��ľ��룮
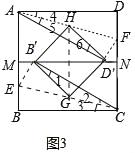
B�⣺��ͼ3����M��AB���е㣬MN��BC��CD�ڵ�N������B'��D��������MN��ʱ��
���ж�B��G��D��H��������ϵ��λ�ù�ϵ����˵�����ɣ�
��ֱ��д����ʱ��H��G֮��ľ��룮

���𰸡���1��֤������������2��A��B��A�⣺��B��G=D��H��B��G��D��H����GH=8��4![]() ��
��
B�⣺��B��G=D��H��B��G��D��H����GH= 4![]() ��4��
��4��
��������
��1�����������ε����ʣ���ת�����ʣ��ɵ�BE=BE�䣬��CB��E=��ABC=90�㣬Ȼ����ݡ�ֱ��������б���ϵ����ߣ�30�Ƚ�����ֱ�DZ�Ϊб�ߵ�һ�롱����֤���ı���BEB��G����������2��A�⣺����ͼ2�����������ε�����ͨ�����߽DZߡ���֤��BCE�ա�ADF��SAS�����ɵ�CE=AF����3=��4��������ת��������ֱ��������б���ϵ�����Ϊб�ߵ�һ��ɵ�B��G=D��H������ƽ���ߵ��ж���֤B��G��D��H��
������GH�����ı���AEGH��ƽ���ı��Σ�����AE=GH����BE=EB��=m����AE=![]() m���ɵù���m�ķ���m+
m���ɵù���m�ķ���m+![]() m=4������ⷽ�̼��ɣ�
m=4������ⷽ�̼��ɣ�
B�⣺����ͼ3���ó��Ľ��������˼·ͬA���е��٣�
������GH�����ı���AEGH��ƽ���ı��Σ���Rt��CNB���У����ù��ɶ������NB��=2![]() ����MB��=4��2
����MB��=4��2![]() ����BE=EB��=y����R��EMB��������y2=��2��y��2+��4��2
����BE=EB��=y����R��EMB���У�����y2=��2��y��2+��4��2![]() ��2��Ȼ����ⷽ�̣�������GH=AE=AB��BE���ɵõ���.
��2��Ȼ����ⷽ�̣�������GH=AE=AB��BE���ɵõ���.
��1��֤������ͼ1�У�
���ı���ABCD�������Σ�
���ABC=90�㣬
���۵���֪��BE=BE�䣬��CB��E=��ABC=90�㣬
��Rt��BCE��Rt��ECB����
��EG=GC��
��BG=![]() EC��GB��=
EC��GB��=![]() EC��
EC��
��BG=GB�䣬
��Rt��BCE��
�ߡ�BCE=30�㣬
��BE=![]() CE��
CE��
��BE=EB��=B��G=BG��
���ı���BEB��G��������
��2��ѡA��B��
A�⣺�����ۣ�B��G=D��H��B��G��D��H��
���ɣ���ͼ2�У�
�ɣ�1���õ���B��G=![]() CE��
CE��
����G��CE���е㣬
��CG=![]() CE��
CE��
��B��G=CG��
���1=��2��
���ı���ABCD�������Σ�
���B=��D=90�㣬AD=BC��
��BE=DF��
���BCE�ա�ADF��SAS����
��CE=AF����3=��4��
���۵���֪����D=��AD��F=90�㣬��2=��3����4=��5��
���2=��5=��1��
��Rt��AD��F��
��H��AF���е㣬
��D��H=AH=![]() AF��
AF��
��B��G=D��H����5=��6��
���1=��6��
��B��G��D��H��
������GH�����ı���AEGH��ƽ���ı��Σ�
��AE=GH����BE=EB��=m����AE=![]() m��
m��
��m+![]() m=4��
m=4��
��m=4![]() ��4��
��4��
��GH=AE=8��4![]() ��
��
B�⣺�����ۣ�B��G=D��H��B��G��D��H��
���ɣ�
�ɣ�1���õ���B��G=![]() CE��
CE��
����G��CE���е㣬
��CG=![]() CE��
CE��
��B��G=CG��
���1=��2��
���ı���ABCD�������Σ�
���B=��D=90�㣬AD=BC��AD��BC��
��BE=DF��
���BCE�ա�ADF��SAS����
��CE=AF����3=��4��
���۵���֪����D=��AD��F=90�㣬��2=��3����4=��5��
���2=��5=��1��
��Rt��AD��F��
��H��AF���е㣬
��D��H=AH=![]() AF��
AF��
��B��G=D��H����5=��6��
���1=��6��
��MN��BC��
��MN��BC��AD��
���AD��M=��DAD��=2��4����CB��N=��BCB��=2��3��
���AD��M=��CB��N��
���AD��M+��6=��CB��N+��1��
����HD��M=��GB��N��
��B��G��D��H��
������GH�����ı���AEGH��ƽ���ı��Σ�
��AE=GH��
��Rt��CNB����CB��=4��CN=2��
��NB��=2![]() ��
��
��MB��=4��2![]() ��
��
��BE=EB��=y��
��R��EMB��������y2=��2��y��2+��4��2![]() ��2��
��2��
��y=8��4![]() ��
��
��GH=AE=AB��BE=4![]() ��4��
��4��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�