题目内容
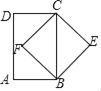
【题目】如图,在矩形ABCD内有一点F,FB与FC分别平分∠ABC和∠BCD,点E为矩形ABCD外一点,连接BE,CE.现添加下列条件:①EB∥CF,CE∥BF;②BE=CE,BE=BF;③BE∥CF,CE⊥BE;④BE=CE,CE∥BF,其中能判定四边形BECF是正方形的共有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
根据题意可得CF=BF,∠F=90°,根据平行四边形与正方形的的判定即可判断①;根据菱形与正方形的判定即可判断②;根据矩形与正方形的判定即可判断③;根据正方形的判定即可判断.
∵四边形ABCD是矩形,
∴∠DCB=∠ABC=90°,
∵FB与FC分别平分∠ABC和∠BCD,
∴∠FCB=![]() ∠DCB=45°,∠FBC=
∠DCB=45°,∠FBC=![]() ∠ABC=45°,
∠ABC=45°,
∴∠FCB=∠FBC=45°,
∴CF=BF,∠F=180°﹣45°﹣45°=90°,
①∵EB∥CF,CE∥BF,
∴四边形BFCE是平行四边形,
∵CF=BF,∠F=90°,
∴四边形BFCE是正方形,故①正确;
∵BE=CE,BF=BE,CF=BF,
∴BF=CF=CE=BE,
∴四边形BFCE是菱形,
∵∠F=90°,
∴四边形BFCE是正方形,故②正确;
∵BE∥CF,CE⊥BE,
∴CF⊥CE,
∴∠FCE=∠E=∠F=90°,
∴四边形BFCE是矩形,
∵BF=CF,
∴四边形BFCE是正方形,故③正确;
∵CE∥BF,∠FBC=∠FCB=45°,
∴∠ECB=∠FBC=45°,∠EBC=∠FCB=45°,
∵∠F=90°,
∴∠FCE=∠FBE=∠F=90°,
∵BF=CF,
∴四边形BFCE是正方形,故④正确;
即正确的个数是4个.
故选:D.

练习册系列答案
相关题目