题目内容
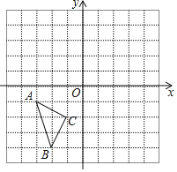
【题目】在如图所示的平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(–3,–1).
(1)将△ABC先沿x轴向右平移3个单位,再沿y轴向上平移2个单位得到△A1B1C1,画出△A1B1C1,并写出点B1坐标.
(2)画出△A1B1C1关于y轴对称的△A2B2C2,并写出点C2的坐标.
(3)求出△A2B2C2的面积.
【答案】(1)作图见解析,B1(1,﹣2);(2)作图见解析,C2(﹣2,0);(3)![]() .
.
【解析】
(1)直接利用平移的性质得出对应点位置进而得出答案;
(2)直接利用轴对称的性质得出对应点位置进而得出答案;
(3)结合△A2B2C2所在矩形面积减去周围三角形面积进而得出答案.
(1)如图所示:△A1B1C1,即为所求,点B1的坐标为:(1,﹣2);
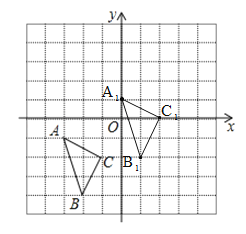
(2)如图所示:△A2B2C2,即为所求,点C2的坐标为:(﹣2,0);
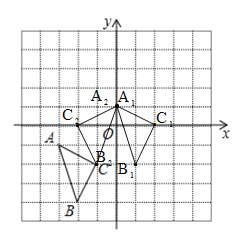
(3)△A2B2C2的面积为:2×3﹣![]() ×2×1﹣
×2×1﹣![]() ×2×1﹣
×2×1﹣![]() ×1×3=
×1×3=![]() .
.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
【题目】某学校开展“文明礼仪”演讲比赛,八(1)班、八(2)班派出的5名选手的比赛成绩如图所示.
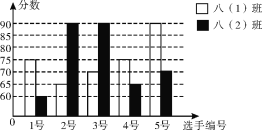
(1)根据上图,完成表格.
平均数 | 中位数 | 方差 | |
八(1)班 | 75 | _______ | _______ |
八(2)班 | 75 | 70 | 160 |
(2)结合两班选手成绩的平均数和方差,分析两个班级参加比赛的选手的成绩.
(3)如果在每班参加比赛的选手中分别选出3人参加决赛,从平均分看,你认为哪个班的实力更强一些?并说明理由.