题目内容
【题目】如图,△ABC中,∠B=65°,∠BAD=40°,∠AED=100°,∠CDE=45°,求∠CAD的度数.
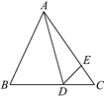
【答案】20°
【解析】
在△ABD中,由内角和定理求得∠BDA=180°-(∠B+∠BAD)=75°,由平角定义知∠ADE=60°,再在△ADE中,由∠CAD=180°-∠ADE-∠AED可得答案.
在△ABD中,因为∠B=65°,∠BAD=40°,
所以∠BDA=180°-(∠B+∠BAD)=180°-(65°+40°)=75°,
因为∠CDE=45°,
所以∠ADE=180°-(∠BDA+∠CDE)=180°-(75°+45°)=60°,
在△ADE中,
因为∠AED=100°,
所以∠CAD=180°-∠ADE-∠AED=180°-60°-100°=20°.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目