题目内容
【题目】如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 . 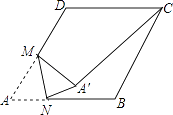
【答案】![]() ﹣1
﹣1
【解析】解:如图所示:∵MA′是定值,A′C长度取最小值时,即A′在MC上时, 过点M作MF⊥DC于点F,
∵在边长为2的菱形ABCD中,∠A=60°,M为AD中点,
∴2MD=AD=CD=2,∠FDM=60°,
∴∠FMD=30°,
∴FD= ![]() MD=
MD= ![]() ,
,
∴FM=DM×cos30°= ![]() ,
,
∴MC= ![]() =
= ![]() ,
,
∴A′C=MC﹣MA′= ![]() ﹣1.
﹣1.
故答案为: ![]() ﹣1.
﹣1.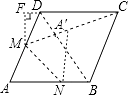
根据题意,在N的运动过程中A′在以M为圆心、AD为直径的圆上的弧AD上运动,当A′C取最小值时,由两点之间线段最短知此时M、A′、C三点共线,得出A′的位置,进而利用锐角三角函数关系求出A′C的长即可.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目