题目内容
37、如图，⊙O1与⊙O2外切于点C，一条外公切线切两圆于点A，B，已知⊙O1的半径是9，⊙O2的半径是3，求∠BAC的度数．分析：作直角梯形的另一高．根据锐角三角函数求得∠O1的度数，再根据弦切角定理求解．
解答：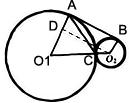
解：作O2D⊥O1A，
在直角三角形O2O1D中，O2O1=9+3=12，O1D=9-3=6，
则∠O1=60°，
根据弦切角定理，得到∠BAC=30°．
解：作O2D⊥O1A，在直角三角形O2O1D中，O2O1=9+3=12，O1D=9-3=6，
则∠O1=60°，
根据弦切角定理，得到∠BAC=30°．
点评：此题要构造直角三角形，根据锐角三角函数的知识和弦切角定理进行求解．
练习册系列答案
相关题目
12、已知：如图，⊙O1与⊙O2外切于点P，直线AB过点P交⊙O1于A，交⊙O2于B，点C、D分别为⊙O1、⊙O2上的点，且∠ACP=65°，则∠BDP=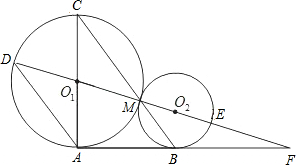
已知：如图，⊙O1与⊙O2外切于M点，AF是两圆的外公切线，A、B是切点，DF经过O1、O2，分别交⊙O1于D、⊙O2于E，AC是⊙O1的直径，BC经过M点，连接AD．
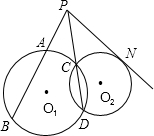如图，⊙O1与⊙O2相交于C、D两点，⊙O1的割线PAB与DC的延长线交于点P，PN与⊙O2相切于点N，若PB=10，AB=6，则PN=
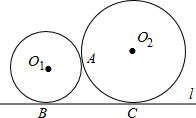已知：如图，⊙O1与⊙O2外切于A点，直线l与⊙O1、⊙O2分别切于B，C点，若⊙O1的半径r1=2cm，⊙O2的半径r2=3cm．求BC的长．
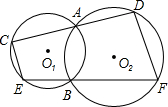已知如图：⊙O1与⊙O2相交于AB两点，过点A、B的直线分别与⊙O1交于C、E，与⊙O2交于D、F，连接CE、DF．