Question

【题目】如图，在中，，，点是重心，连结并延长交于点；连结并延长交于点，过点作交于点.若的面积为8，则的面积为（ ）

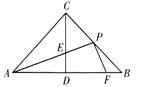
A.4B.2C.1D.

Answer 1

【答案】B

【解析】

连接DP,利用重心性质得DP∥AC,CE：ED=2：1，则△DEP∽△CEA,DP：AC=1：2，再证明△DEP≌△BFP，然后根据相似三角形的面积比等于相似比的平方即可得解．

解：连接DP,∵E是△ABC的重心，
∴CE：DE=2：1，DP∥AC,
∴△DPE∽△CAE，∴DP：AC=1：2.

又AC=BC，∠ACB=90°，D为AB的中点，P为BC的中点，

∴∠B=45°，DP=AC,BP=BC,∴BP=DP①,

∵DP∥AC,∴∠BPD=∠ACB=90°，∠PDC=∠ACD=45°，

∴∠B=∠PDE②，

又∠APF=90°，∴∠DPE+∠DPF=∠BPF+∠DPF,

∴∠DFE=∠BPF③，

由①②③可得，△DEP≌△BFP（ASA）.

∴

∵△ACE面积为8，
∴△BPF的面积为2．
故选：B．