题目内容
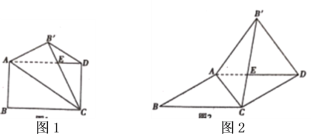
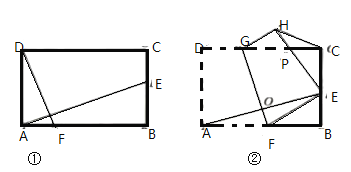
【题目】(1)如图①,在矩形![]() 中,
中,![]() 分别是
分别是![]() 上的点,且
上的点,且![]() ,求
,求![]() 的值;
的值;
(2)如图②,在矩形![]() 中
中![]() (
(![]() 为常数),将矩形
为常数),将矩形![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,得到四边形
处,得到四边形![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的值;
的值;
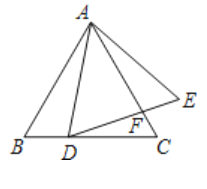
(3)在(2)的条件下,连接![]() ,当
,当![]() 时,若
时,若![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)①证明![]() ,利用相似三角形的性质可求出
,利用相似三角形的性质可求出![]() 的值;
的值;
②作![]() 于点
于点![]() ,证明
,证明![]() ,利用相似三角形的性质可求出
,利用相似三角形的性质可求出![]() 的值;
的值;
(2)结论:![]() .如图2中,作GM⊥AB于M.证明:△ABE∽△GMF即可解决问题.
.如图2中,作GM⊥AB于M.证明:△ABE∽△GMF即可解决问题.
(3)先根据余角的性质证明∠BFE=∠CGH,设![]() ,根据勾股定理求出k,再证明△BFE∽△CEP,即可求解.
,根据勾股定理求出k,再证明△BFE∽△CEP,即可求解.
(1)![]() 四边形
四边形![]() 是矩形,
是矩形,
∴![]() ,∠ABC=∠BAD=90°,
,∠ABC=∠BAD=90°,
![]() ,
,
![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)如图②中,作![]() 于点
于点![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
∴![]() ;
;
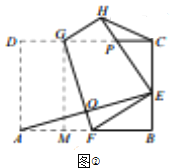
(3)∵∠CGH+∠GPH=90°,∠CEP+∠CPE=90°,
∴∠CGH=∠CEP,
同理∠BFE=∠CEP,
∴∠BFE=∠CGH,
![]() ,
,
设![]() ,
,
![]() ,
,
![]() .
.
![]() 在
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() 或
或![]() (舍去),
(舍去),
![]() ,BF=4,AB=9,
,BF=4,AB=9,
![]() ,
,
∴BC=6,
∴CE=6-3=3,
∠BFE=∠CEP,∠B=∠PEC,
∴△BFE∽△CEP,
∴![]() ,
,
∴![]() ,
,
∴CP=![]() .
.

练习册系列答案
相关题目