题目内容
【题目】抛物线y=ax2+bx+3经过点A(﹣1,0),B(3,0),与y轴交于点C.点D(xD,yD)为抛物线上一个动点,其中1<xD<3.连接AC,BC,DB,DC.
(1)求该抛物线的解析式;
(2)当△BCD的面积等于△AOC的面积的2倍时,求点D的坐标;
(3)在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形.若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)抛物线的解析式为y=﹣x2+2x+3;(2)点D坐标(2,3);(3)M坐标(1,0)或(![]() ,0)或(﹣
,0)或(﹣![]() ,0)或(5,0)
,0)或(5,0)
【解析】
(1)利用待定系数法求函数解析式;
(2)根据解析式先求出△AOC的面积,设点D(xD,yD),由直线BC的解析式表示点E的坐标,求出DE的长,再由△BCD的面积等于△AOC的面积的2倍,列出关于xD 的方程得到点D的坐标;
(3)设点M(m,0),点N(x,y),分两种情况讨论:当BD为边时或BD为对角线时,列中点关系式解答.
解:(1)∵抛物线y=ax2+bx+3经过点A(﹣1,0),B(3,0),
∴![]() ,
,
解得: ![]()
∴抛物线的解析式为y=﹣x2+2x+3;
(2)如图,过点D作DH⊥x轴,与直线BC交于点E,
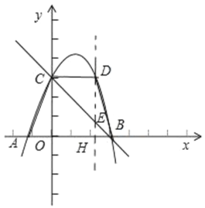
∵抛物线y=﹣x2+2x+3,与y轴交于点C,
∴点C(0,3),
∴OC=3,
∴S△AOC=![]() ×1×3=
×1×3=![]() ,
,
∵点B(3,0),点C(0,3)
∴直线BC解析式为y=﹣x+3,
∵点D(xD,yD),
∴点E(xD,﹣xD+3),yD=﹣xD2+2xD+3,
∴DE=﹣xD2+2xD+3﹣(﹣xD+3)=﹣xD2+3xD,
∴S△BCD=3=![]() ×DE×3,
×DE×3,
∵△BCD的面积等于△AOC的面积的2倍
∴2=﹣xD2+3xD,
∴xD=1(舍去),xD=2,
∴点D坐标(2,3);
(3)设点M(m,0),点N(x,y)
当BD为边,四边形BDNM是平行四边形,
∴BN与DM互相平分,
∴![]() ,
, ![]()
∴y=3,
∴3=﹣x2+2x+3
∴x=2(不合题意),x=0
∴点N(0,3)
∴![]() ,
,
∴m=1,
当BD为边,四边形BDMN是平行四边形,
∴BM与DN互相平分,
∴![]() ,
, ![]()
∴y=﹣3,
∴﹣3=﹣x2+2x+3
∴x=1±![]() ,
,
∴![]() ,
,
∴m=±![]() ,
,
当BD为对角线,
∴BD中点坐标(![]() ,
,![]() ),
),
∴![]() ,
, ![]() ,
,
∴y=3,
∴3=﹣x2+2x+3
∴x=2(不合题意),x=0
∴点N(0,3)
∴m=5,
综上所述点M坐标(1,0)或(![]() ,0)或(﹣
,0)或(﹣![]() ,0)或(5,0).
,0)或(5,0).