题目内容
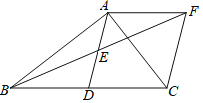
【题目】如图,△ABC中,∠ABC=90°,BA=BC=2,将△ABC绕点C逆时针旋转60°得到△DEC,连接BD,则BD2的值是_____.
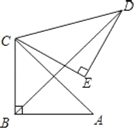
【答案】8+4![]()
【解析】
连接AD,由旋转的性质可得CA=CD,∠ACD=60°,得到△ACD为等边三角形,由AB=BC,CD=AD,得出BD垂直平分AC,于是求出BO=![]() AC=
AC=![]() ,OD=CDsin60°=
,OD=CDsin60°=![]() ,可得BD=BO+OD,即可求解.
,可得BD=BO+OD,即可求解.
如图,连接AD,设AC与BD交于点O,
由题意得:CA=CD,∠ACD=60°
∴△ACD为等边三角形,
∴AD=CD,∠DAC=∠DCA=∠ADC=60°;
∵∠ABC=90°,AB=BC=2,
∴AC=CD=![]() ,
,
∵AB=BC,CD=AD,
∴BD垂直平分AC,
∴BO=![]() AC=
AC=![]() ,OD=CDsin60°=
,OD=CDsin60°=![]() ,
,
∴BD=![]() +
+![]() ,
,
∴BD2=(![]() +
+![]() )2=8+4
)2=8+4![]() ,
,
故答案为8+4![]()

【题目】一个滑道由滑坡(AB段)和缓冲带(BC段)组成,如图所示,滑雪者在滑坡上滑行的距离y(单位:m)和滑行时间t1(单位:s)满足二次函数关系,并测得相关数据:
滑行时间t1/s | 0 | 1 | 2 | 3 | 4 |
滑行距离y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
滑雪者在缓冲带上滑行的距离y2(单位:m)和在缓冲带上滑行时间t2(单位:s)满足:y2=52t2﹣2t22,滑雪者从A出发在缓冲带BC上停止,一共用了23s,则滑坡AB的长度( )米
A.270B.280C.375D.450
【题目】今年上半年,住房和城乡建设等9部门决定在全国地级以上城市全面启动生活垃分类工作.圾分类有利于对垃圾进行分流处理,势在必行.为了了解同学们对垃圾分类相关知识的掌握情况,增强同学们的环保意识,西街中学团委对七年级一,二两班各69名学生进行了垃极分类相关知识的测试,并分别抽取了15份成绩,整理分析过程如下,请补充完整.
(收集数据)
一班15名学生测试成绩统计如下:(满分100分)
68,72,89,85,82,85,74,92,80,85,78,85,69,76,80
二班15名学生测试成绩统计如下:(满分100分)
86,89,83,76,73,78,67,80,80,79,80,84,82,80,83
(整理数据)
(1)按如下分数段整理、描述这两组样本数据
组别 频数 | 65.5~70.5 | 70.5~75.5 | 75.5~80.5 | 80.5~85.5 | 85.5~90.5 | 90.5~95.5 |
一 | 2 | 2 | 4 | 5 | 1 | 1 |
二 | 1 | 1 | a | b | 2 | 0 |
在表中,a= ,b= .
(分析数据)
(2)两组样本数据的平均数、众数、中位数、方差如下表所示:
班级 | 平均数 | 众数 | 中位数 | 方差 |
一 | 80 | x | 80 | 47.6 |
二 | 80 | 80 | y | z |
在表中:x= ,y= .
(3)若规定得分在80分及以上(含80分)为合格,请估计二班69名学生中垃极分类及投放相关知识合格的学生有 人.
(4)你认为哪个班的学生掌握垃圾分类相关知识的整体水平较好,说明理由.