题目内容
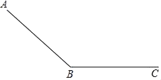
【题目】一个滑道由滑坡(AB段)和缓冲带(BC段)组成,如图所示,滑雪者在滑坡上滑行的距离y(单位:m)和滑行时间t1(单位:s)满足二次函数关系,并测得相关数据:
滑行时间t1/s | 0 | 1 | 2 | 3 | 4 |
滑行距离y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
滑雪者在缓冲带上滑行的距离y2(单位:m)和在缓冲带上滑行时间t2(单位:s)满足:y2=52t2﹣2t22,滑雪者从A出发在缓冲带BC上停止,一共用了23s,则滑坡AB的长度( )米
A.270B.280C.375D.450
【答案】A
【解析】
设y1=a t12+bt1,把(1,4.5)和(2,14)代入函数解析即可求解,y2=52t﹣2t2,函数在对称轴上取得最大值,即滑雪者停下,求出t值,即可求解.
设y1=a t12+bt1,
把(1,4.5)和(2,14)代入函数解析式得![]() ,
,
解得:![]() ,
,
∴二次函数解析式为:y1=2.5 t12+2t1…①;
y2=52t﹣2t2函数在对称轴上取得最大值,即滑雪者停下,
此时,t=![]() =13,
=13,
则:滑雪者在AB段用的时间为2313=10,
把t=10代入①式,
解得:则AB=y1=270(米),
故选:A.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目