题目内容
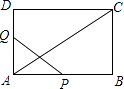
【题目】完成推理填空：如图，已知 AB∥CD，GH平分∠AGM，MN平分∠CMG，请说明GH⊥MN的理由．
解：因为 AB∥CD（已知），
所以∠AGF+ ＝180°（ ），
因为 GH 平分∠AGF，MN 平分∠CMG（ ），
所以∠1＝ 
∠AGF，∠2＝ ∠CMG（ ），
得∠1+∠2＝（∠AGF+∠CMG）＝ ，
所以 GH⊥MN（ ）．
【答案】∠CMG；两直线平行，同旁内角互补；已知；角平分线的定义；90°；垂直的定义．
【解析】
根据平行线的性质（两直线平行，同旁内角互补）、以及角平分线的定义去转化角度即可．
解：因为 AB∥CD（已知），
所以∠AGF+ ∠CMG ＝180°（ 两直线平行，同旁内角互补 ），
因为 GH 平分∠AGF，MN 平分∠CMG（ 已知 ），
所以∠1＝ 
∠AGF，∠2＝ ∠CMG（ 角平分线的定义 ），
得∠1+∠2＝（∠AGF+∠CMG）＝ 90° ，
所以 GH⊥MN（ 垂直的定义 ）．
练习册系列答案
相关题目
