题目内容
【题目】在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/秒的速度移动,点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P、Q同时出发,用t(秒)表示运动时间(0≤t≤6),那么当t为何值时,△APQ与△ABD相似?说明理由. 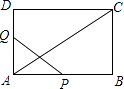
【答案】解:设AP=2tcm,DQ=tcm,
∵AB=12cm,AD=6cm,
∴AQ=(6﹣t)cm,
∵∠A=∠A,
∴①当 ![]() =
= ![]() 时,△APQ∽△ABD,
时,△APQ∽△ABD,
∴ ![]() =
= ![]() ,
,
解得:t=3;
②当 ![]() =
= ![]() 时,△APQ∽△ADB,
时,△APQ∽△ADB,
∴ ![]() =
= ![]() ,
,
解得:t=1.2.
∴当t=3或1.2时,△APQ与△ABD相似
【解析】由题意可设AP=2tcm,DQ=tcm,又由AB=12cm,AD=6cm,即可求得AQ的值,然后分别从①当 ![]() =
= ![]() 时,△APQ∽△ABD;与②当
时,△APQ∽△ABD;与②当 ![]() =
= ![]() 时,△APQ∽△ADB,然后利用方程即可求得t的值.
时,△APQ∽△ADB,然后利用方程即可求得t的值.
【考点精析】本题主要考查了矩形的性质和相似三角形的判定的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)才能正确解答此题.

【题目】某商场的运动服装专柜,对![]() 两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
第一次 | 第二次 | |
| 20 | 30 |
| 30 | 40 |
累计采购款/元 | 10200 | 14400 |
(1)问![]() 两种品牌运动服的进货单价各是多少元?
两种品牌运动服的进货单价各是多少元?
(2)由于![]() 品牌运动服的销量明显好于
品牌运动服的销量明显好于![]() 品牌,商家决定采购
品牌,商家决定采购![]() 品牌的件数比
品牌的件数比![]() 品牌件数的
品牌件数的![]() 倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件
倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件![]() 品牌运动服?
品牌运动服?