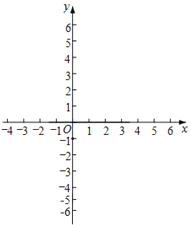题目内容
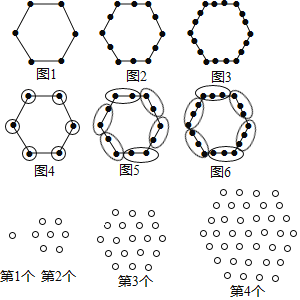
【题目】“分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.例如:图1有6个点,图2有12个点,图3有18个点,……,按此规律,求图10、图n有多少个点?
我们将每个图形分成完全相同的6块,每块黑点的个数相同(如图),这样图1中黑点个数是6×1=6个;图2中黑点个数是6×2=12个:图3中黑点个数是6×3=18个;……;所以容易求出图10、图n中黑点的个数分别是60、6n.
请你参考以上“分块计数法”,先将下面的点阵进行分块,再完成以下问题:
(1)第5个点阵中有 个圆圈;第n个点阵中有 个圆圈.
(2)小圆圈的个数会等于271吗?如果会,请求出是第几个点阵.
【答案】(1)61,3n2﹣3n+1;(2)小圆圈的个数会等于271,它是第10个点阵
【解析】
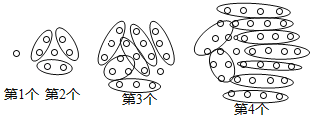
(1)第2个图中2个小圆圈为一块,分为3块,余1,第3个图中3个小圆圈为一块,分为6块,余1;按此规律得:第5个图中5个小圆圈为一块,分为12块,余1,由此即可求得第n个点阵图中小圆圈的个数;
(2)代入271,列方程,方程有解则存在这样的点阵.
解:(1)如图所示:第1个点阵中有:1个,
第2个点阵中有:2×3 ×(2-1)+1=7个,
第3个点阵中有:3×3 ×(3-1)+1=19个,
第4个点阵中有:4×3 ×(4-1)+1=37个,
第5个点阵中有:5×3 ×(5-1)+1=61个,
…
第n个点阵中有:n×3(n﹣1)+1=3n2﹣3n+1,
故答案为:61,3n2﹣3n+1;
(2)3n2﹣3n+1=271,
n2﹣n﹣90=0,
(n﹣10)(n+9)=0,
n1=10,n2=﹣9(舍),
∴小圆圈的个数会等于271,它是第10个点阵.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案【题目】(本题满分10分)科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表):
温度 | …… | -4 | -2 | 0 | 2 | 4 | 4.5 | …… |
植物每天高度增长量 | …… | 41 | 49 | 49 | 41 | 25 | 19.75 | …… |
由这些数据,科学家推测出植物每天高度增长量![]() 是温度
是温度![]() 的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由;
(2)温度为多少时,这种植物每天高度的增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度![]() 应该在哪个范围内选择?请直接写出结果.
应该在哪个范围内选择?请直接写出结果.
【题目】国家教育部提出“每天锻炼一小时,健康工作五十年,幸福生活一辈子”.万州区某中学对九年级部分学生进行问卷调查“你最喜欢的锻炼项目是什么?”,规定从“打球”,“跑步”,“游泳”,“跳绳”,“其他”五个选项中选择自己最喜欢的项目,且只能选择一个项目,并将调查结果绘制成如下两幅不完整的统计图.
最喜欢的锻炼项目 | 人数 |
打球 | 120 |
跑步 |
|
游泳 |
|
跳绳 | 30 |
其他 |
|
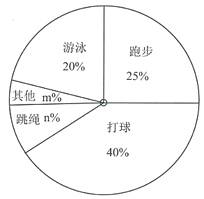
(1)这次问卷调查的学生总人数为 ,人数![]() ;
;
(2)扇形统计图中,![]() ,“其他”对应的扇形的圆心角的度数为 度;
,“其他”对应的扇形的圆心角的度数为 度;
(3)若该年级有1200名学生,估计喜欢“跳绳”项目的学生大约有多少人?
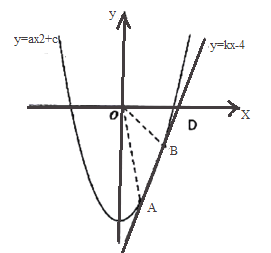
【题目】有这样一个问题:探究函数y=(x﹣1)(x﹣2)(x﹣3)的图象与性质.小东对函数y=(x﹣1)(x﹣2)(x﹣3)的图象与性质进行了探究.下面是小东的探究过程,请补充完成:
(1)函数y=(x﹣1)(x﹣2)(x﹣3)的自变量x的取值范围是_______;
(2)下表是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y | … | m | ﹣24 | ﹣6 | 0 | 0 | 0 | 6 | 24 | 60 | … |
①m=_____;
②若M(﹣7,﹣720),N(n,720)为该函数图象上的两点,则n=_____;
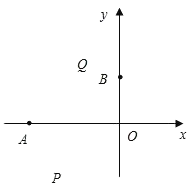
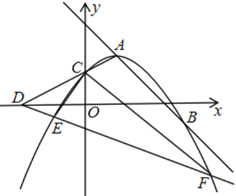
(3)在平面直角坐标系xOy中,A(xA,yA),B(xB,﹣yA)为该函数图象上的两点,且A为2≤x≤3范围内的最低点,A点的位置如图所示.
①标出点B的位置;
②画出函数y=(x﹣1)(x﹣2)(x﹣3)(0≤x≤4)的图象.
③写出直线y=![]() x﹣1与②中你画出图象的交点的横坐标之和为______.
x﹣1与②中你画出图象的交点的横坐标之和为______.