Question

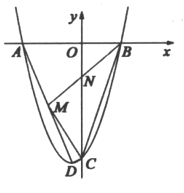
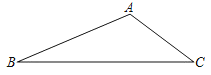
【题目】如图，线段BC和动点A构成△ABC，∠BAC=120°，BC=3，则△ABC周长的最大值_____．

Answer 1

【答案】3+2

【解析】

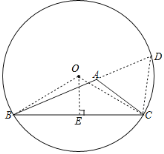
延长BA到D，使AD=AC，连接CD，作△BCD的外接圆⊙O，当BD的长度最大时，△ABC周长最大，而BD为⊙O的直径时，BD最大．设⊙O的半径为r，连接OB，OC，过点O作OE⊥BC于点E，根据垂径定理得出BE的长，再用正弦函数得出OB的长度，则BD的最大值可得，从而△ABC周长的最大值可得．

延长BA到D，使AD=AC，连接CD，作△BCD的外接圆⊙O，

∵AD=AC，

∴△ABC的周长为：AB+BC+AC=AB+BC+AD=BD+BC．

∵BC=3，

∴当BD的长度最大时，△ABC周长最大，

∴当点A与点O重合时，BD为⊙O的直径，BD最大．

设⊙O的半径为r，连接OB，OC，过点O作OE⊥BC于点E，

∵∠BAC=120°，

∴∠BOE=∠AOB=60°．

∵BC=3，OE⊥BC，

∴BE=，

∴=sin60°，

∴

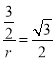
∴r=，

∴BD的最大值为2r=2．

∴△ABC周长的最大值为3+2．

故答案为：3+2．