题目内容
【题目】我们定义:有一组邻边相等且有一组对角互补的凸四边形叫做等补四边形
(1)概念理解
①根据上述定义举一个等补四边形的例子:
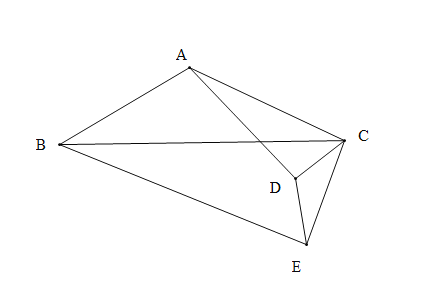
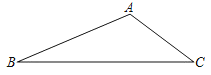
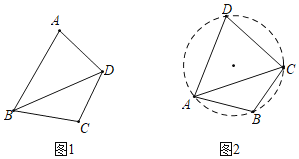
②如图1,四边形ABCD中,对角线BD平分∠ABC,∠A+∠C=180°,求证:四边形ABCD是等补四边形
(2)性质探究:
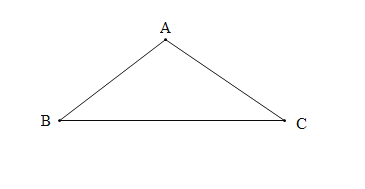
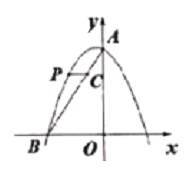
③小明在探究时发现,由于等补四边形有一组对角互补,可得等补四边形的四个顶点共圆,如图2,等补四边形ABCD内接于⊙O,AB=AD,则∠ACD ∠ACB(填“>”“<”或“=“);
④若将两条相等的邻边叫做等补四边形的“等边”,等边所夹的角叫做“等边角”,它所对的角叫做“等边补角”连接它们顶点的对角线叫做“等补对角线”,请用语言表述③中结论:
(3)问题解决
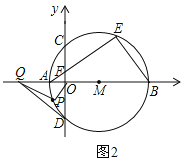
在等补四边形ABCD中,AB=BC=2,等边角∠ABC=120°,等补对角线BD与等边垂直,求CD的长.
【答案】(1)①正方形;②详见解析;(2)③=;④等补四边形的“等补对角线”平分“等边补角”;(3)CD的值为2或4.
【解析】
(1)①正方形是等补四边形.②如图1中,作DM⊥BA于M,DN⊥BC于N,则∠DMA=∠DNC=90°,证明△ADM≌△CDN(AAS),推出AD=DC,即可解决问题.
(2)③根据弦,弧,圆周角之间的关系解决问题即可.④根据“等补对角线”,“等边补角”等定义,利用③中结论即可解决问题.
(3)分两种情形:①如图3﹣1中,当BD⊥AB时.②如图3﹣2中,当BD⊥BC时,分别求解即可.
(1)①解:正方形是等补四边形.
②证明:如图1中,作DM⊥BA于M,DN⊥BC于N,则∠DMA=∠DNC=90°,

∵∠A+∠BCD=180°,∠BCD+∠DCN=180°,
∴∠A=∠DCN,
∵BD平分∠ABC,
∴DM=DN,
在△ADM和△CDN中,
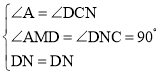 ,
,
∴△ADM≌△CDN(AAS),
∴AD=DC,
∴四边形ABCD是等补四边形.
(2)③解:如图2中,
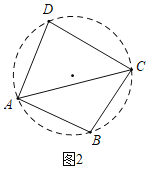
∵AD=AB,
∴![]() =
=![]() ,
,
∴∠ACD=∠ACB.
故答案为=.
④解:由题意,等补四边形的“等补对角线”平分“等边补角”.
故答案为等补四边形的“等补对角线”平分“等边补角”.
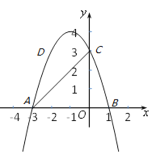
(3)解:如图3﹣1中,当BD⊥AB时,

∵∠ADC+∠ABC=180°,∠ABC=120°,
∴∠ADC=60°,
∵∠ABD=90°,
∴AD是⊙O的直径,
∴∠ACD=90°,
∴∠DAC=∠DBC=30°,
∵BA=BC,∠ABC=120°,
∴∠BAC=∠ACB=30°,
∴∠BAC=∠BDC=30°,
∴∠CBD=∠CDB,
∴DC=BC=2.
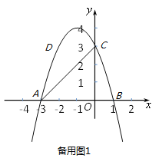
如图3﹣2中,当BD⊥BC时,
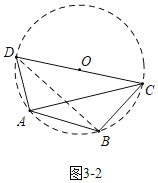
∵∠DBC=90°,
∴CD是⊙O的直径,
∵BA=BC,∠ABC=120°,
∴∠BAC=∠ACB=30°,
∴∠BAC=∠BDC=30°,
∴CD=2BC=4,
综上所述,满足条件的CD的值为2或4.

 天天练口算系列答案
天天练口算系列答案