ÌâÄ¿ÄÚÈÝ
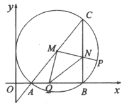
¡¾ÌâÄ¿¡¿Èçͼ£¬ÔÚÁâÐÎABCDÖУ¬¶Ô½ÇÏß![]() ÏཻÓÚµãM£¬ÒÑÖª
ÏཻÓÚµãM£¬ÒÑÖª![]() £¬µãEÔÚÉäÏß
£¬µãEÔÚÉäÏß![]() ÉÏ£¬
ÉÏ£¬![]() £¬µãP´ÓµãB³ö·¢£¬ÒÔÿÃë
£¬µãP´ÓµãB³ö·¢£¬ÒÔÿÃë![]() ¸öµ¥Î»µÄËÙ¶ÈÑØBD·½ÏòÏòÖÕµãDÔÈËÙÔ˶¯£¬¹ýµã
¸öµ¥Î»µÄËÙ¶ÈÑØBD·½ÏòÏòÖÕµãDÔÈËÙÔ˶¯£¬¹ýµã![]() ×÷
×÷![]() ½»ÉäÏß
½»ÉäÏß![]() ÓÚµã
ÓÚµã![]() £¬ÒÔ
£¬ÒÔ![]() ΪÁڱ߹¹ÔìƽÐÐËıßÐÎ
ΪÁڱ߹¹ÔìƽÐÐËıßÐÎ![]() £¬Éèµã
£¬Éèµã![]() µÄÔ˶¯Ê±¼äΪ
µÄÔ˶¯Ê±¼äΪ![]() £»
£»
£¨1£©![]() £»
£»
£¨2£©Çóµã![]() ÂäÔÚ
ÂäÔÚ![]() ÉÏʱ
ÉÏʱ![]() µÄÖµ£»
掙术
£¨3£©ÇóƽÐÐËıßÐÎ![]() Óë
Óë![]() Öصþ²¿·ÖÃæ»ýSÓë
Öصþ²¿·ÖÃæ»ýSÓë![]() Ö®¼äµÄº¯Êý¹Øϵʽ£»
Ö®¼äµÄº¯Êý¹Øϵʽ£»
£¨4£©Á¬½ÓƽÐÐËıßÐÎ![]() µÄ¶Ô½ÇÏß
µÄ¶Ô½ÇÏß![]() £¬Éè
£¬Éè![]() Óë
Óë![]() ½»ÓÚµã
½»ÓÚµã![]() £¬Á¬½Ó
£¬Á¬½Ó![]() £¬µ±
£¬µ±![]() Óë
Óë![]() µÄ±ßƽÐУ¨²»Öغϣ©»ò´¹Ö±Ê±£¬Ö±½Óд³ö
µÄ±ßƽÐУ¨²»Öغϣ©»ò´¹Ö±Ê±£¬Ö±½Óд³ö![]() µÄÖµ£®
µÄÖµ£®
¡¾´ð°¸¡¿£¨1£©![]() £»£¨2£©
£»£¨2£©![]() £»£¨3£©
£»£¨3£©![]() £¬S£½
£¬S£½![]() £¬S=
£¬S=![]() £»£¨4£©tֵΪ
£»£¨4£©tֵΪ![]() »ò
»ò![]() »ò
»ò![]() »ò2£®
»ò2£®
¡¾½âÎö¡¿
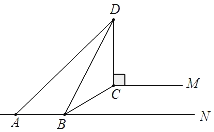
£¨1£©Èçͼ£¬×÷DH¡ÍBEÓÚH£¬½âÖ±½ÇÈý½ÇÐÎÇó³öBH£¬DH¼´¿É£®
£¨2£©ÈçͼÓÉPF¡ÎCB£¬¿ÉµÃ![]() £¬¹¹Ôì·½³Ì¼´¿É½âµÃ£®
£¬¹¹Ôì·½³Ì¼´¿É½âµÃ£®
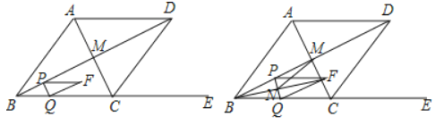
£¨3£©·ÖÈýÖÖÇé¿ö£¬µ±0£¼t¡Ü![]() ʱ£¬Öصþ²¿·ÖΪƽÐÐËıßÐÎPBQF£»µ±
ʱ£¬Öصþ²¿·ÖΪƽÐÐËıßÐÎPBQF£»µ±![]() £¼t¡Ü1ʱ£¬Öصþ²¿·ÖΪÎå±ßÐÎPBQRT£»µ±1£¼t¡Ü2ʱ£¬Öصþ²¿·ÖΪËıßÐÎPBCT,·Ö±ðÇó½â½â¾ö¼´¿É£®
£¼t¡Ü1ʱ£¬Öصþ²¿·ÖΪÎå±ßÐÎPBQRT£»µ±1£¼t¡Ü2ʱ£¬Öصþ²¿·ÖΪËıßÐÎPBCT,·Ö±ðÇó½â½â¾ö¼´¿É£®
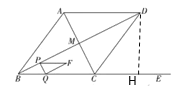
£¨4£©·ÖËÄÖÖÇé¿ö£ºµ±MN¡ÎABʱ£¬ÉèCM½»BFÓÚT£»µ±MN¡ÍBCʱ£»µ±MN¡ÍABʱ£»µ±PµãÓëDµãÖغÏʱ£¬MN¡ÎBC£¬·Ö±ð¾Í³ö¼´¿É£®
½â£º£¨1£©Èçͼ×öDH¡ÍBEÓÚH,
ÔÚRt¡÷BCDÖУ¬
¡ßDHC=![]() £¬CD=5
£¬CD=5
tan¡ÏDCH=![]()
¡àDH=4£¬CH=3
¡àBH=BC+CH=5+3=8
¡àtan¡ÏDBE=![]() =
=![]()
£¨2£©ÈçÏÂͼ
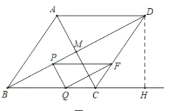
¡ßËıßÐÎABCDÊÇÁâÐÎ
¡àAC¡ÍBD
¡ßBC=5£¬tan¡ÏCBM=![]()
¡àCM=![]() £¬BM=DM=
£¬BM=DM=![]()
¡ßPF¡ÎCB
¡à![]()
¡à![]()
½âµÃt=![]() £®
£®
£¨3£©ÈçÏÂͼ
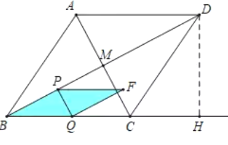
µ±0£¼t¡Ü![]() £¬Öصþ²¿·ÖΪƽÐÐËıßÐÎPBQF£¬
£¬Öصþ²¿·ÖΪƽÐÐËıßÐÎPBQF£¬
S=PB¡ÁPQ=![]()
ÈçÏÂͼ£¬
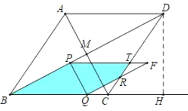
µ±![]() £¼t¡Ü1ʱ£¬Öصþ²¿·ÖÊÇÎå±ßÐÎPBQRT£¬
£¼t¡Ü1ʱ£¬Öصþ²¿·ÖÊÇÎå±ßÐÎPBQRT£¬
S=![]()
=![]() £®
£®
ÈçÏÂͼ
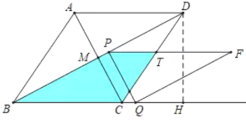
µ±1£¼t¡Ü2ʱ£¬Öصþ²¿·ÖÊÇËıßÐÎPBCT
S=![]()
=![]()
£¨4£©ÈçÏÂͼ£¬µ±MN¡ÎABʱ£¬ÉèCM½»BFÓÚT
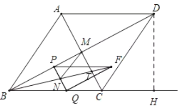
¡ßPN¡ÎMT
¡à![]()
¡à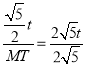
¡àMT=![]()
¡ßMN¡ÎAB
¡à![]()
¡à![]()
¡à![]()
¡àt=![]() £»
£»
ÈçÏÂͼ
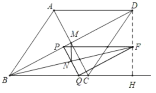
µ±MN¡ÍBCʱ£¬Ò×ÖªµãFÔÚDHÉÏ
¡ßPF¡ÎBH£¬
¡à![]()
¡à![]()
½âµÃt=![]() £»
£»
ÈçÏÂͼ
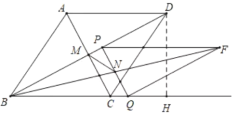
µ±MN¡ÍABʱ£¬Ò×Öª¡ÏPNM=¡ÏABD
¿ÉµÃtan¡ÏPNM=![]()
¡à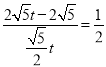
½âµÃt=![]()
µ±µãPÓëµãDÖغÏʱ£¬MN¡ÎBC£¬´Ëʱt=2
×ÛÉÏËùÊö£¬Âú×ãÌõ¼þµÄtֵΪ![]() »ò
»ò![]() »ò
»ò![]() »ò2£®
»ò2£®