ЬтФПФкШн
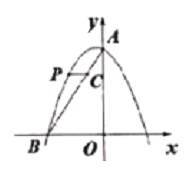
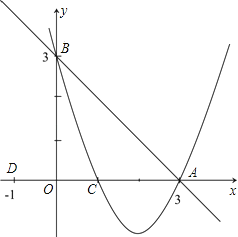
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§LгыyжсНЛгкЕуC(0ЃЌ3)ЃЌЧвЙ§Еу(1ЃЌ0)ЃЌ(3ЃЌ0)ЃЎ
(1)ЧѓЖўДЮКЏЪ§LЕФНтЮіЪНМАЖЅЕуHЕФзјБъ
(2)вбжЊxжсЩЯЕФФГЕуM(tЃЌ0)ЃЛШєХзЮяЯпLЙигкЕуMЖдГЦЕФаТХзЮяЯпЮЊLЁфЃЌЧвЕуCЁЂHЕФЖдгІЕуЗжБ№ЮЊCЁфЃЌHЁфЃЛЪдЫЕУїЫФБпаЮCHCЁфHЁфЮЊЦНааЫФБпаЮЃЎ
(3)ШєЦНааЫФБпаЮЕФБпгыФГвЛЬѕЖдНЧЯпЛЅЯрДЙжБЪБЃЌГЦетжжЦНааЫФБпаЮЮЊЁАКЭаГЫФБпаЮЁБЃЛдк(2)ЕФЬѕМўЯТЃЌЕБЦНааЫФБпаЮCHCЁфHЁфЮЊЁАКЭаГЫФБпаЮЁБЪБЃЌЧѓtЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ y=x2Љ4x+3ЃЌ(2,Љ1)ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉ t=![]() Лђ4ЛђЉ6
Лђ4ЛђЉ6
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓНтЮіЪНЃЌгЩХфЗНЗЈПЩЧѓЖЅЕузјБъЃЛ
ЃЈ2ЃЉгЩжааФЖдГЦЕФаджЪПЩЕУCM=C'MЃЌHM=H'MЃЌПЩЕУНсТлЃЛ
ЃЈ3ЃЉЗжЫФжжЧщПіЬжТлЃЌгЩСНЕуОрРыЙЋЪНКЭвЛДЮКЏЪ§ЕФаджЪПЩЧѓНтЃЎ
ЃЈ1ЃЉЩшЖўДЮКЏЪ§LЕФНтЮіЪНЮЊЃКy=ax2+bx+c(aЁй0)
гЩЬтвтПЩЕУЃК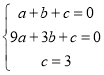
НтЕУЃК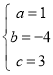
ЁрЖўДЮКЏЪ§LЕФНтЮіЪНЮЊЃКy=x2Љ4x+3ЃЌ
Ёпy=x2Љ4x+3=(xЉ2)2Љ1ЃЌ
ЁрЖЅЕуHЕФзјБъ(2,Љ1)
ЙЪД№АИЮЊЃКy=x2Љ4x+3ЃЌ(2,Љ1)
ЃЈ2ЃЉ
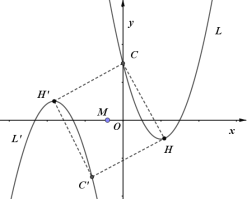
ЁпШєХзЮяЯпLЙигкЕуMЖдГЦЕФаТХзЮяЯпЮЊLЁфЃЌЧвЕуCЁЂHЕФЖдгІЕуЗжБ№ЮЊCЁфЃЌHЁфЃЛ
ЁрCM=C'MЃЌHM=H'MЃЌ
ЁрЫФБпаЮCHCЁфHЁфЮЊЦНааЫФБпаЮЃЛ
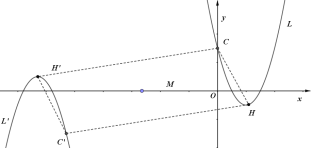
ЃЈ3ЃЉЁпЕуC(0,3)ЃЌЕуH(2,Љ1)
ЁржБЯпCHНтЮіЪНЮЊЃКy=Љ2x+3ЃЛ
ШєCC'ЁЭCHЪБЃЌдђCC'НтЮіЪНЮЊЃК![]()
ЕБy=0ЪБЃЌ![]()
Ёрt=Љ6ЃЛ
ШєHH'ЁЭCHЪБЃЌдђHH'НтЮіЪНЮЊЃК![]()
ЕБy=0ЪБЃЌ![]()
Ёрt=4
ЁпШєХзЮяЯпLЙигкЕуMЖдГЦЕФаТХзЮяЯпЮЊLЁфЃЌЧвЕуCЁЂHЕФЖдгІЕуЗжБ№ЮЊCЁфЃЌHЁфЃЛ
ЁрЕуC'(2tЃЌЉ3)ЃЌЕуH'(2tЉ2ЃЌ1)
ШєCH'ЁЭHH'ЃЌдђH'C2+H'H2=CH2ЃЌ
Ёр(2tЉ2Љ0)2+(3Љ1)2+(2tЉ2Љ2)2+(1+1)2=(0Љ2)2+(3+1)2ЃЌ
Ёрt=![]()
ШєCC'ЁЭCH'ЃЌдђH'C2+C'C2=C'H'2ЃЌ
Ёр(2tЉ2Љ0)2+(3Љ1)2+(2tЉ0)2+(3+3)2=(0Љ2)2+(3+1)2ЃЌ
ЁрЁїЃМ0ЃЌЗНГЬЮоНтЃЛ
злЩЯЫљЪіЃКt=![]() Лђ4ЛђЉ6ЃЎ
Лђ4ЛђЉ6ЃЎ
ЙЪД№АИЮЊЃКt=![]() Лђ4ЛђЉ6ЃЎ
Лђ4ЛђЉ6ЃЎ

 БИеНжаПМКЎМйЯЕСаД№АИ
БИеНжаПМКЎМйЯЕСаД№АИ