题目内容
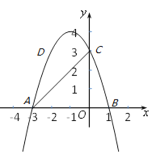
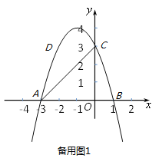
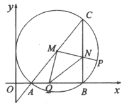
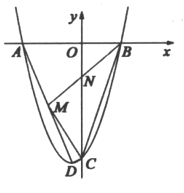
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与x轴交于
与x轴交于![]() 、B两点,与y轴交点C的坐标为
、B两点,与y轴交点C的坐标为![]() ,
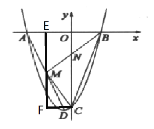
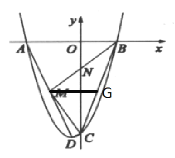
,![]() 为抛物线顶点,连结AD,点M为线段AD上动点(不含端点),BM与y轴交于点N.
为抛物线顶点,连结AD,点M为线段AD上动点(不含端点),BM与y轴交于点N.
(1)求抛物线解析式;
(2)是否存在点M使得![]() 与
与![]() 相似,若存在请求出点M的坐标,若不存在,请说明理由;
相似,若存在请求出点M的坐标,若不存在,请说明理由;
(3)求当BM将四边形ABCM分为面积相等的两部分时ON的长度.
【答案】(1)![]() (2)存在,M坐标为
(2)存在,M坐标为![]() ,
,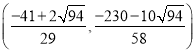 ,
, ;(3)
;(3)![]()
【解析】
(1)将![]() 代入解析式
代入解析式![]() 解方程即可;
解方程即可;
(2)两三角形相似有两种对应关系,当![]() 时满足题意,设M坐标代入AC解析式即可,当
时满足题意,设M坐标代入AC解析式即可,当![]() 时也满足题意,根据相似三角形列比例式求解即可;
时也满足题意,根据相似三角形列比例式求解即可;
(3)设点M坐标,利用铅垂线法求两个三角形面积,利用相等条件列方程求解即可.
解:(1)将![]() 代入解析式
代入解析式![]() 得:
得:
![]() ,
,
解得:![]() ,
,
∴抛物线解析式为![]() ;
;
(2)存在
理由:![]() ,
,
![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
将![]() 代入得,
代入得,
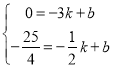 ,
,
解得: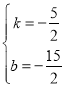 ,
,
∴直线![]() 解析式为
解析式为![]() ,
,
当![]() 时,
时,
![]() ,
,![]() ,
,
设![]() ,代入
,代入![]() 得,
得,
![]() ,
,
解得:![]() ,
,
![]() ;
;
当![]() 时,
时,![]() ,
,
作直线![]() 轴交x轴与点E,作直线
轴交x轴与点E,作直线![]() 交ME轴与点F,
交ME轴与点F,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,又
,又![]() ,
,
∴可得![]() ,
,
![]() ,
,
![]() ,
,
即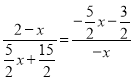 ,
,
解得:![]() ,
,
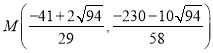 或
或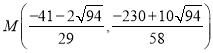 ,
,
综上当M坐标为![]() ,
,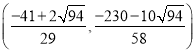 ,
, 时,满足题意;
时,满足题意;
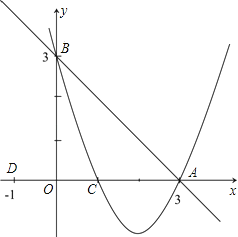
(3)作![]() 轴交
轴交![]() 于点G,
于点G,
设直线BC解析式为![]() ,
,
将![]() 代入解析式得,
代入解析式得,
![]() ,
,
解得![]() ,
,
∴直线BC解析式为![]() ,
,
设![]() ,
,
则![]() ,
,
将![]() 代入直线BC解析式得,
代入直线BC解析式得,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
由题意得![]() ,
,
解得![]() ,
,
![]() ,
,
设直线BM的解析式为![]() ,
,
将![]() 代入BM解析式得,
代入BM解析式得,
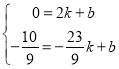 ,
,
解得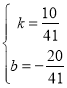 ,
,
![]() ,
,
![]()

【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级成绩频数分布直方图:

b.七年级成绩在![]() 这一组的是:70 72 74 75 76 76 77 77 77 78 79
这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.