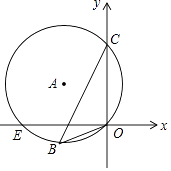题目内容
【题目】如图，已知抛物线y=﹣x2+2x+3与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，连接BC．
（1）求A、B、C三点的坐标及抛物线的对称轴；
（2）若已知x轴上一点N（ 
，0），则在抛物线的对称轴上是否存在一点Q，使得△CNQ是直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．
【答案】
（1）解：由y=﹣x2+2x+3得到：y=﹣（x+1）（x﹣3），或y=﹣（x﹣1）2+4，
则A（﹣1，0），B（3，0），对称轴是x=1．
令x=0，则y=3，
所以C（0，3），
综上所述，A（﹣1，0），B（3，0），C（0，3），对称轴是x=1
（2）解：假设存在满足条件的点Q．
设Q（1，m）．
又（0，3），
∴CN2=32+（ 
）2= 
，CQ2=12+（3﹣m）2=m2﹣6m+10．NQ2=（ ﹣1）2+m2= 
+m2．
①当点C是直角顶点时，则CN2+CQ2=NQ2，即 +m2﹣6m+10= +m2．
解得m= 
，
此时点Q的坐标是（1， ）；
②当点N为直角顶点时，CN2+NQ2=CQ2，即 + +m2=m2﹣6m+10
解得m=﹣ ，
此时点Q的坐标是（1，﹣ ）；
③当点Q为直角顶点时，CQ2+NQ2=CN2，即 = +m2+m2﹣6m+10
解得m= 
或m= 
，
此时点Q的坐标是（1， ）或（1， ）．
综上所述，满足条件的点Q的坐标为：（1， ）或（1，﹣ ）或（1， ）或（1， ）
【解析】（1）分别令y=0,x=0,可求出抛物线与x轴、y轴交点坐标；利用对称轴公式x=-
,求出对称轴；（2）“是否存在”问题的基本解决方案法为：假设存在满足条件的点Q，△CNQ是直角三角形可分为三类：①当点C是直角顶点时②当点N为直角顶点时③当点Q为直角顶点时，再利用勾股定理列出方程，得出答案.
