题目内容
【题目】问题呈现：
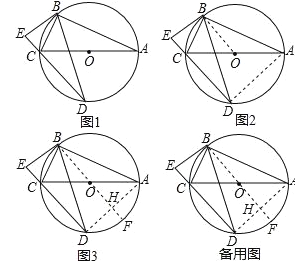
如图1，⊙O是Rt△ABC的外接圆，∠ABC=90°，弦BD=BA，BE⊥DC交DC的延长线于点E．求证：BE是⊙O的切线．
问题分析：
连接OB，要证明BE是⊙O的切线，只要证明OB ____ BE，由题意知∠E=90°，故只需证明OB ___ DE．
解法探究：
（1）小明对这个问题进行了如下探索，请补全他的证明思路：
如图2，连接AD，由∠ECB是圆内接四边形ABCD的一个外角，可证∠ECB=∠BAD，因为OB=OC，所以 __ ，因为BD=BA，所以 ______ ，利用同弧所对的圆周角相等和等量代换，得到 ____ ，所以DE∥OB，从而证明出BE是⊙O的切线．
（2）如图3，连接AD，作直径BF交AD于点H，小丽发现BF⊥AD，请说明理由．
（3）利用小丽的发现，请证明BE是⊙O的切线．（要求给出两种不同的证明方法）．
【答案】问题分析：⊥，∥（1）∠CBO=∠BCO，∠BAD=∠BDA，∠ECB=∠CBO（2）BF⊥AD（3）证明见解析
【解析】
试题分析：问题分析：直接得出结论即可；
解法探究：（1）根据证明方法直接写出结论；
（2）先判断出OD=OA，再用垂径定理即可得出结论；
（3）方法1，先判断出AC是⊙O的直径，进而判断出四边形BEDH是矩形即可；
方法2，先判断出AH=DH，再判断出AC是⊙O的直径，进而判断出OH是△ACD的中位线，即可得出DE∥OB，即可得出结论；
试题解析：问题分析：
故答案为：⊥，∥；
解法探究：
（1）故答案为：∠CBO=∠BCO，∠BAD=∠BDA，∠ECB=∠CBO；
（2）如图3，
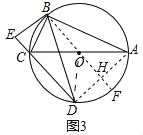
连接OD，
∴OD=OA，
∵BD=BA，
∴BF垂直平分AD，
即：BF⊥AD（垂径定理），
（3）方法1，∵BF⊥AD，
∴∠BHD=90°，
∵∠ABC=90°，
∴AC是⊙O的直径，
∴∠ADC=90°，
∵∠E=90°，
∴四边形BEDH是矩形，
∴∠EBO=90°，
∴BE是⊙O的切线；
方法2，∵BF⊥AD，
∴AH=DH（垂径定理），
∵∠ABC=90°，
∴AC是⊙O的直径，
∴AO=CO，
∴OH是△ACD的中位线，
∴OH∥DC，
即：DE∥OB，
∵∠E=90°，
∴∠EBO=90°，
∴BE是⊙O的切线．
