题目内容
如图,函数y=-x+4的图象分别交x轴,y轴于点N、M,过MN上的两点A、B分别向x轴作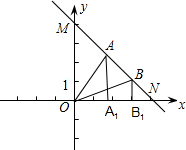 垂线,与x轴交于A1(x1,0),B1(x2,0),A1在B1的左边,若OA1+OB1>4.
垂线,与x轴交于A1(x1,0),B1(x2,0),A1在B1的左边,若OA1+OB1>4.(1)分别用含x1、x2的代数式表示△OA1A的面积S1与△OB1B的面积S2.
(2)请判断△OA1A的面积S1与△OB1B的面积S2的大小关系,并说明理由.
分析:(1)本题须先设出A、B的坐标,再分别用x1、x2表示出OA1A1AOB1B1B的长即可得出结果.
(2)本题须先求出S1-S2的值,再通过结果的符号即可判断出S1、S2的大小.
(2)本题须先求出S1-S2的值,再通过结果的符号即可判断出S1、S2的大小.
解答:解:设A(x1,y1),B(x2,y2),则y1=-x1+4,y2=-x2+4.
(1)S1=
OA1•A1A=
x1(-x1+4)=-
+2x1.S2=
OB1•B1B=
x2(-x2+4)=-
+2x2.
(2)S1>S2.
理由如下:S1-S2=-
(
-
)+2(x1-x2)=-
(x1-x2)(x1+x2-4).
由题意知x1<x2,且x1+x2>4.所以,x1-x2<0,x1+x2-4>0.
可得S1-S2>0,即S1>S2.
(1)S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x | 2 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x | 2 2 |
(2)S1>S2.
理由如下:S1-S2=-
| 1 |
| 2 |
| x | 2 1 |
| x | 2 2 |
| 1 |
| 2 |
由题意知x1<x2,且x1+x2>4.所以,x1-x2<0,x1+x2-4>0.
可得S1-S2>0,即S1>S2.
点评:本题主要考查了一次函数的综合应用,在解题时要注意把一次函数的性质与三角形的面积求法相结合是本题的关键.

练习册系列答案
相关题目
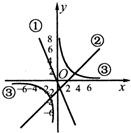 如图,函数图象①、②、③的表达式应为( )
如图,函数图象①、②、③的表达式应为( )A、y=-
| ||||
B、y=
| ||||
C、y=-
| ||||
D、y=-
|
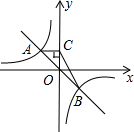 如图:函数y=-kx(k≠0)与y=-
如图:函数y=-kx(k≠0)与y=-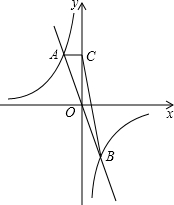 如图,函数y=-kx与
如图,函数y=-kx与 如图,函数y1=k1x+b的图象与函数y2=
如图,函数y1=k1x+b的图象与函数y2=