题目内容
【题目】在矩形
的各边
、
、
和
上分别选取点
、
、
、
，使得
，如果
，
，四边形
的最大面积是（ ）.
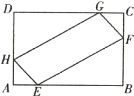
A.1350B.1300
C.1250D.1200
【答案】C
【解析】
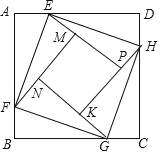
设AE=x，四边形EFGH的面积是S，则AH=CF=CG=x．分别求出矩形四个角落的三角形的面积，再利用矩形的面积减去四个角落的三角形的面积，可得四边形EFGH的面积S；先配方，确定函数的对称轴，再与函数的定义域结合即可求出四边形EFGH的面积最大值．
设AE=x，四边形EFGH的面积是S，则AH=CF=CG=x．
由题意，BE=DG=60﹣x，BF=DH=40﹣x，则
S△AHE=S△CGF
x2，S△DGH=S△BEF（60﹣x）（40﹣x），
所以四边形EFGH的面积为：
S=60×40﹣x2﹣（60﹣x）（40﹣x）=﹣2x2+100x=﹣2（x﹣25）2+1250（0＜x≤40）；
当x=25时，S最大值=1250．
故选C．
练习册系列答案
相关题目
