题目内容
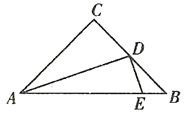
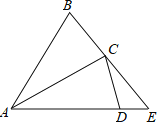
【题目】如图,在△ABC中,AB=AC=2,∠BAC=30°,将△ABC沿AC翻折得到△ACD,延长AD交BC的延长线于点E,则△ABE的面积为( )
A.![]() B.
B.![]() C.3D.
C.3D.![]()
【答案】B
【解析】
由折叠的性质可知∠CAD=30°=∠CAB,AD=AB=2.由等腰三角形的性质得出∠BCA=∠ACD=∠ADC=75°.求出∠ECD=30°.由三角形的外角性质得出∠E=75°﹣30°=45°,过点C作CH⊥AE于H,过B作BM⊥AE于M,由直角三角形的性质得出CH=![]() AC=1,AH=
AC=1,AH=![]() CH=
CH=![]() .得出HD=AD﹣AH=2﹣
.得出HD=AD﹣AH=2﹣![]() .求出EH=CH=1.得出DE=EH﹣HD=
.求出EH=CH=1.得出DE=EH﹣HD=![]() ﹣1,AE=AD+DE=1+
﹣1,AE=AD+DE=1+![]() ,由直角三角形的性质得出AM=
,由直角三角形的性质得出AM=![]() AB=1,BM=
AB=1,BM=![]() AM=
AM=![]() .由三角形面积公式即可得出答案.
.由三角形面积公式即可得出答案.
解:由折叠的性质可知:∠CAD=30°=∠CAB,AD=AB=2.
∴∠BCA=∠ACD=∠ADC=75°.
∴∠ECD=180°﹣2×75°=30°.
∴∠E=75°﹣30°=45°.
过点C作CH⊥AE于H,过B作BM⊥AE于M,如图所示:
在Rt△ACH中,CH=![]() AC=1,AH=
AC=1,AH=![]() CH=
CH=![]() .
.
∴HD=AD﹣AH=2﹣![]() .
.
在Rt△CHE中,
∵∠E=45°,
∴△CEH是等腰直角三角形,
∴EH=CH=1.
∴DE=EH﹣HD=1﹣(2﹣![]() )=
)=![]() ﹣1,
﹣1,
∴AE=AD+DE=1+![]() ,
,
∵BM⊥AE,∠BAE=∠BAC+∠CAD=60°,
∴∠ABM=30°,
∴AM=![]() AB=1,BM=
AB=1,BM=![]() AM=
AM=![]() .
.
∴△ABE的面积=![]() AE×BM=
AE×BM=![]() ×(1+
×(1+![]() )×
)×![]() =
=![]() ;
;
故选:B.

【题目】我校初二体育考试选择项目中,选择篮球项目和排球项目的学生比较多.为了解学生掌握篮球技巧和排球技巧的水平况,进行了抽样调查,过程如下,请补充完整下题表格.
收集数据:从选择篮球和排球的学生各随机抽取10人,进行了测试,测试成绩如下:
排球9 9.5 9 9 8 10 9.5 8 4 9.5
篮球9.5 9.5 8.5 8.5 10 9.5 6 8 6 9
整理、描述数据:按如下分数段整理、描述这两组样本数据:
项目 人数 成绩x | 4.0≤x<5.5 | 5.5≤x<7.0 | 7.0≤x<8.5 | 8.5≤x<10 | 10 |
排球 | 1 | 0 | 2 | 6 | 1 |
篮球 | 0 | 2 | 1 | 6 | 1 |
(说明:成绩8.5分及以上为优秀,6分及以上为合格,6分以下为不合格.)
分折数据两组样本数据的平均数、中位数、众数如表所示:
项目 | 平均数 | 中位数 | 众数 |
排球 | 8.55 | a | 9和9.5 |
篮球 | 8.45 | 8.75 | b |
应用数据
(1)填空:a= ,b= .
p>(2)初三年级的小伟和小明看到上面数据后,小伟说:排球项目整体水平较高:小明说:篮球项目整体水平较高.你同意 的看法,理由为:① ;② .(从两个不同的角度说明推理的合理性)(3)如果初二年级有180人选排球项目,请信计该年级排球项目获得优秀的人数.