题目内容
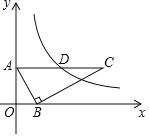
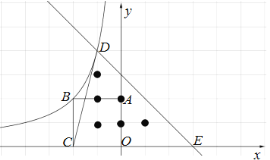
【题目】已知:如图,在平面直角坐标系xOy中,点A(0,2),正方形OABC的顶点B在函数![]() (k ≠ 0,x<0) 的图象上,直线
(k ≠ 0,x<0) 的图象上,直线![]() :
:![]() 与函数
与函数![]() (k ≠ 0,x<0) 的图象交于点D,与x轴交于点E.
(k ≠ 0,x<0) 的图象交于点D,与x轴交于点E.
(1)求k的值;
(2)横、纵坐标都是整数的点叫做整点.
①当一次函数![]() 的图象经过点A时,直接写出△DCE内的整点的坐标;
的图象经过点A时,直接写出△DCE内的整点的坐标;
②若△DCE内的整点个数恰有6个,结合图象,求b的取值范围.

【答案】(1)-4;(2)①(-1,1),(-1,2),(0,1),②2<b≤3
【解析】
(1)依题意得到B(﹣2,2),于是得到结论;
(2)①根据题意求得一次函数的解析式为y=﹣x+2,得到D(1﹣![]() ,1+
,1+![]() ),E(2,0),于是得到结论;
),E(2,0),于是得到结论;
②当b=2时,△DCE内有3个整点,当b=3时,△DCE内有6个整点,即可得到b的取值范围是2<b≤3.
解:(1)依题意知:B(-2,2)
∴反比例函数解析式为![]() .
.
∴k的值为-4.
(2)①∵一次函数y=﹣x+b的图象经过点A,
∴b=2,
∴一次函数的解析式为y=﹣x+2,
∴E(2,0),
解 得,
得, ,
, ,
,
∵x<0
∴D(1﹣![]() ,1+
,1+![]() ),
),
∴△DCE内的整点的坐标为(﹣1,1),(﹣1,2),(0,1);
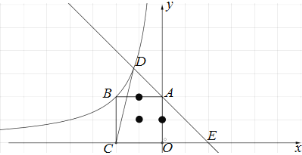
②当b=2时,△DCE内有3个整点,当b=3时,△DCE内有6个整点,
∴b的取值范围是2<b≤3.

练习册系列答案
相关题目