ЬтФПФкШн
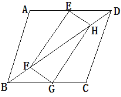
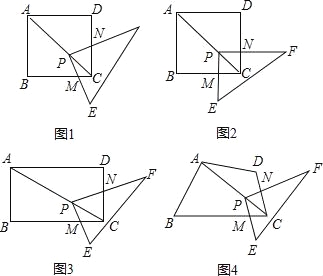
ЁОЬтФПЁПШчЭМ1ЃЌЕуPдке§ЗНаЮABCDЕФЖдНЧЯпACЩЯЃЌе§ЗНаЮЕФБпГЄЪЧaЃЌRtЁїPEFЕФСНЬѕжБНЧБпPEЁЂPFЗжБ№НЛBCЁЂDCгкЕуMЁЂNЃЎ
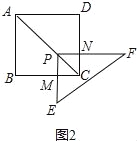
ЃЈ1ЃЉВйзїЗЂЯжЃКШчЭМ2ЃЌЙЬЖЈЕуPЃЌЪЙЁїPEFШЦЕуPа§зЊЃЌЕБPMЁЭBCЪБЃЌЫФБпаЮPMCNЪЧе§ЗНаЮЃЎЬюПеЃКЂйЕБAP=2PCЪБЃЌЫФБпаЮPMCNЕФБпГЄЪЧ_________ЃЛЂкЕБAP=nPCЪБЃЈnЪЧе§ЪЕЪ§ЃЉЃЌЫФБпаЮPMCNЕФУцЛ§ЪЧ__________ЃЎ
ЃЈ2ЃЉВТЯыТлжЄ
ШчЭМ3ЃЌИФБфЫФБпаЮABCDЕФаЮзДЮЊОиаЮЃЌAB=aЃЌBC=bЃЌЕуPдкОиаЮABCDЕФЖдНЧЯпACЩЯЃЌRtЁїPEFЕФСНЬѕжБНЧБпPEЁЂPFЗжБ№НЛBCЁЂDCгкЕуMЁЂNЃЌЙЬЖЈЕуPЃЌЪЙЁїPEFШЦЕуPа§зЊЃЌдђ![]() =_______ЃЎ
=_______ЃЎ
ЃЈ3ЃЉЭиеЙЬНОП
ШчЭМ4ЃЌЕБЫФБпаЮABCDТњзуЬѕМўЃКЁЯB+ЁЯD=180ЁуЃЌЁЯEPF=ЁЯBADЪБЃЌЕуPдкACЩЯЃЌPEЁЂPFЗжБ№НЛBCЃЌCDгкMЁЂNЕуЃЌЙЬЖЈPЕуЃЌЪЙЁїPEFШЦЕуPа§зЊЃЌЧыЬНОП![]() ЕФжЕЃЌВЂЫЕУїРэгЩЃЎ
ЕФжЕЃЌВЂЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй![]() aЃЛЂк
aЃЛЂк![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉМћНтЮіЃЎ
ЃЛЃЈ3ЃЉМћНтЮіЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉЂйШчЭМ2ЃЌЁпPMЁЭBCЃЌABЁЭBЃЌЁрЁїPMCЁзЁїABCЃЌЁр![]() =
=![]() ЃЌгжЁпAP=2PCЃЌЁр
ЃЌгжЁпAP=2PCЃЌЁр![]() =
=![]() ЃЌМД
ЃЌМД![]() =
=![]() ЃЌЁрPM=
ЃЌЁрPM=![]() aЃЌМДе§ЗНаЮPMCNЕФБпГЄЪЧ
aЃЌМДе§ЗНаЮPMCNЕФБпГЄЪЧ![]() aЃЛ
aЃЛ
ЂкЕБAP=nPCЪБЃЈnЪЧе§ЪЕЪ§ЃЉЃЌ![]() =
=![]() ЃЌЁрPM=
ЃЌЁрPM=![]() aЃЌЁрЫФБпаЮPMCNЕФУцЛ§=ЃЈ
aЃЌЁрЫФБпаЮPMCNЕФУцЛ§=ЃЈ![]() aЃЉ2=
aЃЉ2=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ3ЃЌЙ§PзїPGЁЭBCгкGЃЌзїPHЁЭCDгкHЃЌдђЁЯPGM=ЁЯPHN=90ЁуЃЌЁЯGPH=90ЁуЃЌЁпRtЁїPEFжаЃЌЁЯFPE=90ЁуЃЌЁрЁЯGPM=ЁЯHPNЃЌЁрЁїPGMЁзЁїPHNЃЌЁр![]() =
=![]() ЃЌгЩPGЁЮABЃЌPHЁЮADПЩЕУЃЌ
ЃЌгЩPGЁЮABЃЌPHЁЮADПЩЕУЃЌ![]() ЃЌ
ЃЌ
ЁпAB=aЃЌBC=bЃЌЁр![]() ЃЌМД
ЃЌМД![]() =
=![]() ЃЌЁр
ЃЌЁр![]() =
=![]() ЃЛ
ЃЛ

ЃЈ3ЃЉШчЭМ4ЃЌЙ§PзїPGЁЮABЃЌНЛBCгкGЃЌзїPHЁЮADЃЌНЛCDгкHЃЌдђЁЯHPG=ЁЯDABЃЌЁпЁЯEPF=ЁЯBADЃЌЁрЁЯEPF=ЁЯGPHЃЌМДЁЯEPH+ЁЯHPN=ЁЯEPH+ЁЯGPMЃЌЁрЁЯHPN=ЁЯGPMЃЌЁпЁЯB+ЁЯD=180ЁуЃЌЁрЁЯPGC+ЁЯPHC=180ЁуЃЌгжЁпЁЯPHN+ЁЯPHC=180ЁуЃЌЁрЁЯPGC=ЁЯPHNЃЌЁрЁїPGMЁзЁїPHNЃЌЁр![]() =
=![]() ЂйЃЌгЩPGЁЮABЃЌPHЁЮADПЩЕУЃЌ
ЂйЃЌгЩPGЁЮABЃЌPHЁЮADПЩЕУЃЌ![]() =
=![]() =
=![]() ЃЌМД
ЃЌМД![]() =
=![]() ЂкЃЌЁргЩЂйЂкПЩЕУЃЌ
ЂкЃЌЁргЩЂйЂкПЩЕУЃЌ![]() =
=![]() ЃЎ
ЃЎ