题目内容
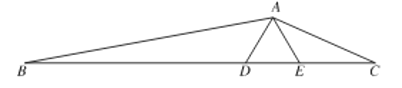
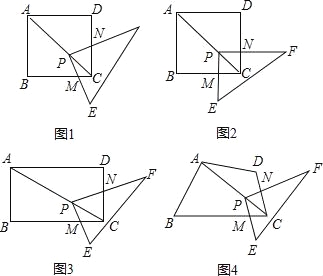
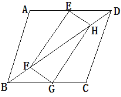
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.
(1)求证:BG=DE.
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
【答案】(1)证明见解析;(2)8.
【解析】
(1)根据矩形的性质得到EH=FG,EH∥FG,得到∠GFH=∠EHF,求得∠BFG=∠DHE,根据菱形的性质得到AD∥BC,得到∠GBF=∠EDH,根据全等三角形的性质即可得到结论;
(2)连接EG,根据菱形的性质得到AD=BC,AD∥BC,求得AE=BG,AE∥BG,得到四边形ABGE是平行四边形,得到AB=EG,于是得到结论.
解:(1)∵四边形EFGH是矩形,
∴EH=FG,EH//FG,
∴∠GFH=∠EHF,
∵∠BFG=180°-∠GFH,∠DHE=180°-∠EHF,
∴∠BFG=∠DHE,
∵四边形ABCD是菱形,
∴AD//BC,
∴∠GBF=∠EDH,
∴△BGF≌△DEH(AAS),
∴BG=DE.
(2)连接EG,∵四边形ABCD是菱形,
∴AD=BC,
∵E为AD中点,
∴AE=ED,
∵BG=DE,
∴AE=BG,AE//BG,
∴四边形ABGE是平行四边形,
∴AB=EG,
∵EG=FH=2,
∴AB=2,
∴菱形ABCD的周长=8.

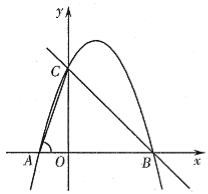
【题目】如图,直线![]() 和
和![]() 相交于点
相交于点![]() ,
,![]() ,在射线
,在射线![]() 上取一点
上取一点![]() ,使
,使![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 是线段
是线段![]() 上的一个动点(不与点
上的一个动点(不与点![]() 重合),过点
重合),过点![]() 作
作![]() 的垂线交射线
的垂线交射线![]() 于点
于点![]() .
.
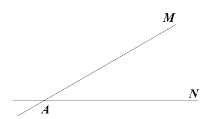
(1)确定点![]() 的位置,在线段
的位置,在线段![]() 上任取一点
上任取一点![]() ,根据题意,补全图形;
,根据题意,补全图形;
(2)设![]() cm,
cm,![]() cm,探究函数
cm,探究函数![]() 随自变量
随自变量![]() 的变化而变化的规律.
的变化而变化的规律.
①通过取点、画图、测量,得到了![]() 与
与![]() 的几组对应值,如下表:
的几组对应值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
(要求:补全表格,相关数值保留一位小数)
②)建立平面直角坐标系![]() ,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;
,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;

③结合画出的函数图象,解决问题:当![]() 为
为![]() 斜边
斜边![]() 上的中线时,
上的中线时,![]() 的长度约为_____cm(结果保留一位小数).
的长度约为_____cm(结果保留一位小数).
【题目】某班数学兴趣小组经过市场调查,整理出某种商品在第![]() 天的售价与销量的相关信息如下表:
天的售价与销量的相关信息如下表:
时间 |
|
|
售价(元/件) |
| 90 |
每天销量(件) |
| |
已知该商品的进价为每件30元,设销售该商品的每天利润为![]() 元
元
(1)求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?