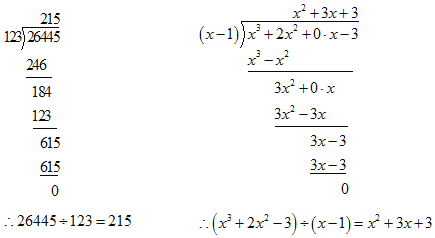题目内容
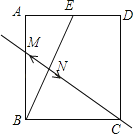
【题目】如图,以△ABC的一边AB为直径作⊙O,交于BC的中点D,过点D作直线EF与⊙O相切,交AC于点E,交AB的延长线于点F.若△ABC的面积为△CDE的面积的8倍,则下列结论中,错误的是( )
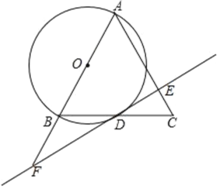
A.AC=2AOB.EF=2AEC.AB=2BFD.DF=2DE
【答案】B
【解析】
连接OD、AD,根据三角形中位线定理判断A选项;根据切线的性质、三角形的面积公式判断B;根据平行线分线段成比例定理判断C、D,即可得到答案.
解:连接OD、AD,
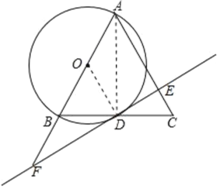
∵OB=OA,BD=DC,
∴AC=2OD,
∵OA=OD,
∴AC=2OD,A正确,不符合题意;
∵EF是⊙O的切线,
∴OD⊥EF,
∵OB=OA,BD=DC,
∴OD∥AC,
∴AE⊥EF,
∵△ABC的面积为△CDE的面积的8倍,D是BC的中点,
∴△ADC的面积为△CDE的面积的4倍,
∴△ADE的面积为△CDE的面积的3倍,
∴AE=3EC,
∴![]() ,
,
∵OD∥AC,
∴![]() ,
,
∴FA=2AE,B错误,符合题意;
AB=2BF,C正确,不符合题意;
∵![]() ,
,
∴DF=2DE,D正确,不符合题意;
故选:B.

练习册系列答案
相关题目
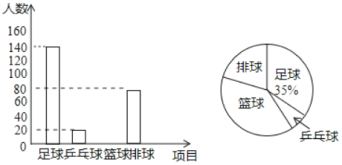
【题目】某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取![]() 进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
运动项目 | 频数(人数) |
羽毛球 | 30 |
篮球 |
|
乒乓球 | 36 |
排球 |
|
足球 | 12 |

请根据以上图表信息解答下列问题:
(1)频数分布表中的![]() ,
,![]() ;
;
(2)在扇形统计图中,“排球”所在的扇形的圆心角为 度;
(3)全校有多少名学生选择参加乒乓球运动?