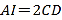Question

【题目】已知抛物线 与x轴只有一个交点，且交点为A（-2,0）.

（1）求b，c的值；

（2）若抛物线与y轴的交点为B，坐标原点为O，求△OAB的面积.

Answer 1

【答案】（1）b＝4，c＝4；（2）4.

【解析】

（1）根据抛物线与x轴只有一个公共点，根据交点是A（-2，0），可得抛物线关于顶点的解析式为y＝（x+2）2，即可得到答案；
（2）当x＝0时，y＝x2+4x+4＝4，则B（0，4），根据直角三角形的面积公式进行计算即可得到答案．

解：（1）∵抛物线y＝x2+bx+c与x轴只有一个交点，且交点为A（﹣2，0），

∴抛物线解析式为y＝（x+2）2，

即y＝x2+4x+4，

∴b＝4，c＝4；

（2）当x＝0时，y＝x2+4x+4＝4，则B（0，4），

∴△OAB的面积＝×2×4＝4．