题目内容
【题目】如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.

(1)求C点坐标;
(2)求直线MN的解析式;
(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
【答案】(1)C(0,6)。
(2)y=![]() x+6。
x+6。
(3)P1(4,3),P2(![]() )P3(
)P3(![]() ),P4(
),P4(![]() )。
)。
【解析】
试题
(1)通过解方程x2﹣14x+48=0可以求得OC=6,OA=8.则C(0,6);
(2)设直线MN的解析式是y=kx+b(k≠0).把点A、C的坐标分别代入解析式,列出关于系数k、b的方程组,通过解方程组即可求得它们的值;
(3)需要分类讨论:PB为腰,PB为底两种情况下的点P的坐标.根据等腰三角形的性质、两点间的距离公式以及一次函数图象上点的坐标特征进行解答.
试题解析:
(1)解方程x2-14x+48=0得
x1=6,x2=8
∵OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根
∴OC=6,OA=8
∴C(0,6)
(2)设直线MN的解析式是y=kx+b(k≠0)
由(1)知,OA=8,则A(8,0)
∵点A、C都在直线MN上
∴![]()
解得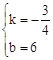 ,
,
∴直线MN的解析式为y=-![]() x+6
x+6
(3)
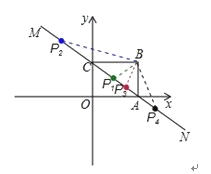
∵A(8,0),C(0,6)
∴根据题意知B(8,6)
∵点P在直线MN y=-![]() x+6上
x+6上
∴设P(a,--![]() a+6)
a+6)
当以点P,B,C三点为顶点的三角形是等腰三角形时,需要分类讨论:
①当PC=PB时,点P是线段BC的中垂线与直线MN的交点,则P1(4,3);
②当PC=BC时,a2+(-![]() a+6-6)2=64
a+6-6)2=64
解得,a=±![]() ,则P2(-
,则P2(-![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() )
)
③当PB=BC时,(a-8)2+(-![]() a+6-6)2=64
a+6-6)2=64
解得,a=![]() ,则-
,则-![]() a+6=-
a+6=-![]()
∴P4(![]() ,
,![]() )
)
综上所述,符合条件的点P有:P1(4,3),P2(-![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() ),P4(
),P4(![]() ,-
,-![]() )
)

【题目】一张长方形桌子可坐6人,按下图方式讲桌子拼在一起.
 ………
………
① ② ③
(1)观察图形,填写下表:
图形(n) | ② | ③ | …… | n |
坐的人数(人) | …… |
(2)一家餐厅有40张这样的长方形桌子,按照上图的方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?
(3)在(2)中,若改为每8张桌子拼成1张大桌子,则共可坐多少人?






