题目内容
如图,Rt△ABC的顶点B在反比例函数y= 的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是
的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是
| A.12 | B.4 | C.12- | D.12-3 |
C.
解析试题分析::∵∠ACB=90°,BC=4,
∴B点纵坐标为4,
∵点B在反比例函数y= 的图象上,
的图象上,
∴当y=4时,x=3,即B点坐标为(3,4),
∴OC=3.
在Rt△ABC中,∠ACB=90°,∠A=30°,BC=4,
∴AB=2BC=8,AC= BC=4
BC=4 ,OA=AC-OC=4
,OA=AC-OC=4 -3.
-3.
设AB与y轴交于点D.
∵OD∥BC,
∴ ,即
,即 ,
,
解得OD=4- ,
,
∴阴影部分的面积是: (OD+BC)•OC=
(OD+BC)•OC= (4-
(4- +4)×3=12-
+4)×3=12-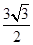 .
.
故选C.
考点:1.反比例函数系数k的几何意义;2.含30度角的直角三角形;3.勾股定理.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知反比例函数y= 的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是( )
的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是( )
| A.(﹣6,1) | B.(1,6) | C.(2,﹣3) | D.(3,﹣2) |
下列各点在双曲线y= 上的是( )
上的是( )
| A.(3,-4) | B.(4,-3) | C.(-2,6) | D.(-2,-6) |
已知反比例函数 的图象如图,则一元二次方程
的图象如图,则一元二次方程 根的情况是( )
根的情况是( )
| A.有两个不等实根 | B.有两个相等实根 | C.没有实根 | D.无法确定. |
下列各点在反比例函数 的图象上的是( )
的图象上的是( )
| A.(-1,-2) | B.(-1,2) | C.(-2,-1) | D.(2,1) |
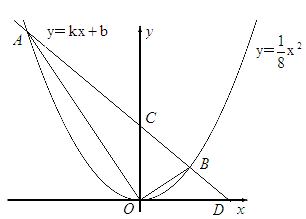
 与抛物线
与抛物线 相交于A
相交于A ,B
,B 两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且
两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且 。
。 在反比例函数
在反比例函数 的图象上;
的图象上;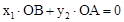 。
。
 和
和 的图象交于A、B两点.若点C是y轴上任意一点,连接AC、BC,则△ABC的面积为( )
的图象交于A、B两点.若点C是y轴上任意一点,连接AC、BC,则△ABC的面积为( )

 与
与 成反比例,且当
成反比例,且当 时,
时, ,那么当
,那么当 时,
时, .
.