题目内容
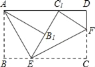
【题目】如图，在长方形ABCD中，AB=8cm，BC=12cm，点E为AB中点，如果点P在线段BC上以每秒4cm的速度，由点B向点C运动，同时，点Q在线段CD上以v厘米/秒的速度，由点C向点D运动，设运动时间为t秒.
（1）直接写出：PC= 厘米，CQ= 厘米；(用含t、v的代数式表示)
（2）若以E、B、P为顶点的三角形和以P、C、Q为顶点的三角形全等，试求v、t的值；
（3）若点Q以（2）中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针方向沿长方形ABCD的四边运动，求经过多长时间点P与点Q第一次在长方形ABCD的哪条边上相遇？
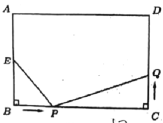
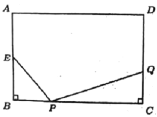
备用图
【答案】（1）12-4t；vt；（2）当BP=CQ时，t=2，v=4；当BP=PC时，t=1.5，v=
；（3）t=9；P、Q相遇在边AD上.
【解析】
（1）根据路程=速度
时间，即可直接写出代数式；
（2）根据△BEP≌△CQP，由全等三角形性质可知，对应边相等，此时对应边不确定，需要分成2种情况进行分类讨论，分别求出答案即可；
（3）依据点P的运动路程，即可得到经过9秒点P与点Q第一次在AB边上相遇．
（1）根据题意得：PC=BC-BP=12-4t，CQ=vt；
故答案为：12-4t，vt.
（2）∵点E是AB中点，
∴BE=4
当BP=CQ时，BE=PC=4，△BEP≌△CQP
∴
，
解得：
；
当BP=PC时，BE=CQ=4，△BEP≌△CQP
∴
，
解得：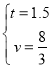
；
（3）根据题意可知，当P、Q两点的速度一样，都是v=4时，点P点与Q点永远不会相遇，故v=4，不符合题意，舍去；
当点P速度为4，点Q速度为
时，点P会与点Q相遇，
此时会有：
解得：
路程：
cm
∵BC=AD=12，CD=AB=8
∴BC+CD+AD=42 cm
∴走过36 cm，点P、Q第一次相遇在AD上.
