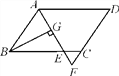
题目内容
【题目】如图,已知![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一动点(与点
上一动点(与点![]() 不重合),
不重合),![]() 分别平分
分别平分![]() 和
和![]() ,分别交射线
,分别交射线![]() 于点
于点![]() .
.

(1)![]() ;
;![]() ;
;
(2)当点![]() 运动到某处时,
运动到某处时,![]() ,求此时
,求此时![]() 的度数.
的度数.
(3)当点![]() 运动时,
运动时,![]() :
:![]() 的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
【答案】(1)100°,50°;(2)25°;(3)∠APB:∠ADB=2:1.
【解析】
(1)由平行线的性质:两直线平行同旁内角互补可得![]() 100°;再根据角平分线的定义可得2∠CBP+2∠DBP=100°,即可得
100°;再根据角平分线的定义可得2∠CBP+2∠DBP=100°,即可得![]() 50°.
50°.
(2)由平行可得∠ACB=∠CBN,结合已知![]() 可得∠ABC=∠CBP=∠DBP=∠DBN即可解决问题;即
可得∠ABC=∠CBP=∠DBP=∠DBN即可解决问题;即![]() =
=![]() =25°.
=25°.
(3)可以证明∠APB=∠PBN,∠ADB=∠DBN=![]() ∠PBN.
∠PBN.
解:(1)∵AM∥BN,∠A=80°,
∴∠A+∠ABN=180°,
∴∠ABN=100°;
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=100°,
∴∠CBD=∠CBP+∠DBP=50°;
故答案为:100°,50°;
(2)∵AM∥BN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠ABD-∠CBD=∠CBN-∠CBD=∠DBN,
∴∠ABC=∠CBP=∠DBP=∠DBN,
∴∠ABC=![]() ∠ABN=
∠ABN=![]() =25°,
=25°,
(3)不变.理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
又∵BD平分∠PBN,
∴∠ADB=∠DBN=![]() ∠PBN=
∠PBN=![]() ∠APB,
∠APB,
即∠APB:∠ADB=2:1.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】供电局的电力维修工甲、乙两人要到30千米远的A地进行电力抢修.甲骑摩托车先行,![]() 小时后乙开抢修车载着所需材料出发,结果甲、乙两人同时到达.已知抢修车的速度是摩托车的1.5倍,求摩托车的速度.
小时后乙开抢修车载着所需材料出发,结果甲、乙两人同时到达.已知抢修车的速度是摩托车的1.5倍,求摩托车的速度.
(1)设摩托车的速度为x千米/时,利用速度、时间、路程之间的关系填写下表.
(要求:填上适当的代数式,完成表格)
速度(千米/时) | 所走的路程(千米) | 所用时间(时) | |
摩托车 | x | 30 | |
抢修车 | 30 |
(2)列出方程,并求摩托车的速度.