题目内容
【题目】如图,在Rt△ABO中,斜边AB=1.若OC∥BA,∠AOC=36°,则( )
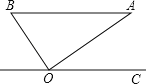
A.点B到AO的距离为sin54°
B.点B到AO的距离为tan36°
C.点A到OC的距离为sin36°sin54°
D.点A到OC的距离为cos36°sin54°
【答案】C
【解析】
试题分析:根据图形得出B到AO的距离是指BO的长,过A作AD⊥OC于D,则AD的长是点A到OC的距离,根据锐角三角形函数定义得出BO=ABsin36°,即可判断A、B;过A作AD⊥OC于D,则AD的长是点A到OC的距离,根据锐角三角形函数定义得出AD=AOsin36°,AO=ABsin54°,求出AD,即可判断C、D.
解:
B到AO的距离是指BO的长,
∵AB∥OC,
∴∠BAO=∠AOC=36°,
∵在Rt△BOA中,∠BOA=90°,AB=1,
∴sin36°=![]() ,
,
∴BO=ABsin36°=sin36°,
故A、B选项错误;
过A作AD⊥OC于D,则AD的长是点A到OC的距离,
∵∠BAO=36°,∠AOB=90°,
∴∠ABO=54°,
∵sin36°=![]() ,
,
∴AD=AOsin36°,
∵sin54°=![]() ,
,
∴AO=ABsin54°,
∵AB=1,
∴AD=ABsin54°sin36°=1×sin54°sin36°=sin54°sin36°,故C选项正确,D选项错误;
故选:C.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目