题目内容
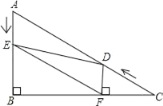
【题目】如图,在Rt△ABC中,∠B=90°,BC=![]() ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)AC的长是 ,AB的长是 .
(2)在D、E的运动过程中,线段EF与AD的关系是否发生变化?若不变化,那么线段EF与AD是何关系,并给予证明;若变化,请说明理由.
(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
【答案】(1)AB=5,AC=10;(2)EF与AD平行且相等;(3)当t=![]() 时,四边形AEFD为菱形
时,四边形AEFD为菱形
【解析】
(1)在Rt△ABC中,∠C=30°,则AC=2AB,根据勾股定理得到AC和AB的值.
(2)先证四边形AEFD是平行四边形,从而证得AD∥EF,并且AD=EF,在运动过程中关系不变.
(3)求得四边形AEFD为平行四边形,进而利用菱形的判定与性质得出AE=AD时,求出t的值,进而得出答案.
(1)解:∵在Rt△ABC中,∠C=30°,
∴AC=2AB,
根据勾股定理得:AC2﹣AB2=BC2,
∴3AB2=75,
∴AB=5,AC=10;
(2)EF与AD平行且相等.
证明:在△DFC中,∠DFC=90°,∠C=30°,DC=2t,
∴DF=t.
又∵AE=t,
∴AE=DF,
∵AB⊥BC,DF⊥BC,
∴AE∥DF.
∴四边形AEFD为平行四边形.
∴EF与AD平行且相等.
(3)解:能;
理由如下:
∵AB⊥BC,DF⊥BC,
∴AE∥DF.
又∵AE=DF,
∴四边形AEFD为平行四边形.
∵AB=5,AC=10.
∴AD=AC﹣DC=10﹣2t.
若使AEFD为菱形,则需AE=AD,
即t=10﹣2t,解得:t=![]() .
.
即当t=![]() 时,四边形AEFD为菱形.
时,四边形AEFD为菱形.
故答案为:(1)AB=5,AC=10;(2)EF与AD平行且相等;(3)当t=![]() 时,四边形AEFD为菱形.
时,四边形AEFD为菱形.

 名校课堂系列答案
名校课堂系列答案【题目】供电局的电力维修工甲、乙两人要到30千米远的A地进行电力抢修.甲骑摩托车先行,![]() 小时后乙开抢修车载着所需材料出发,结果甲、乙两人同时到达.已知抢修车的速度是摩托车的1.5倍,求摩托车的速度.
小时后乙开抢修车载着所需材料出发,结果甲、乙两人同时到达.已知抢修车的速度是摩托车的1.5倍,求摩托车的速度.
(1)设摩托车的速度为x千米/时,利用速度、时间、路程之间的关系填写下表.
(要求:填上适当的代数式,完成表格)
速度(千米/时) | 所走的路程(千米) | 所用时间(时) | |
摩托车 | x | 30 | |
抢修车 | 30 |
(2)列出方程,并求摩托车的速度.