题目内容
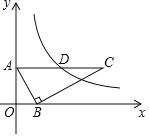
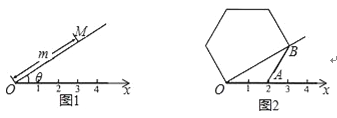
【题目】规定：如图1，在平面内选一定点O，引一条有方向的射线Ox，再选定一个单位长度，那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定，有序数对（θ，m）称为M点的“极坐标”，在图2的极坐标系下，如果正六边形的边长为2，有一边OA在射线Ox上，则正六边形的顶点B的极坐标应记为（ ）
A．（
，30°） B．（60°，
）
C．（30°，4） D．（30°，
）
【答案】D
【解析】
试题分析：如图，过B作BC⊥x轴于C，
∵六边形是正六边形，
∴∠BAC=60°，AO=AB，
∴∠ABC=30°，∠AOB=∠ABO=30°，
∴在Rt△ACB中，BC=
AB=
，
在Rt△BCO中，BO=2BC=
．
∴正六边形的顶点B的极坐标应记为（30°，
）．
故选：D．
练习册系列答案
名校课堂系列答案
相关题目
