题目内容
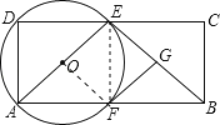
【题目】如图,矩形ABCD中,AB=5,AD=3.点E是CD上的动点,以AE为直径的⊙O与AB交于点F,过点F作FG⊥BE于点G.
(1)若E是CD的中点时,证明:FG是⊙O的切线
(2)试探究:BE能否与⊙O相切?若能,求出此时DE的长;若不能,请说明理由.

【答案】(1)见解析;(2)点E不存在,BE不能与⊙O相切,理由见解析
【解析】
(1)要证明FG是⊙O的切线只要证明OF⊥FG即可;
(2)先假设BE能与⊙O相切,则AE⊥BE,即∠AEB=90°.设DE的长为x,然后用x表示出CE的长,根据勾股定理可得出一个关于x的一元二次方程,若BE能与⊙O相切,那么方程的解即为DE的长;若方程无解,则说明BE不可能与⊙O相切.
(1)连接OF、EF;
∵AE是⊙O的直径,AF⊥EF,
∵四边形ABCD是矩形,
∴∠DAB=∠D=90°,AB=CD,
∴四边形ADEF是矩形,
∴AF=DE,
∴EC=BF,
∵E是CD的中点,
∴F是AB的中点,
∴OF∥BE,
∵FG⊥BE,
∴OF⊥FG,
∴FG为⊙O的切线.
(2)若BE能与⊙O相切,因AE是⊙O的直径,则AE⊥BE,∠AEB=90°.
设DE=x,则EC=5﹣x.
由勾股定理得:AE2+EB2=AB2,
即(9+x2)+[(5﹣x)2+9]=25,
整理得x2﹣5x+9=0,
∵b2﹣4ac=25﹣36=﹣11<0,
∴该方程无实数根,
∴点E不存在,BE不能与⊙O相切.

练习册系列答案
相关题目