题目内容
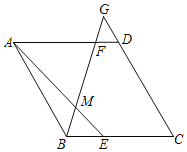
【题目】如图,点P是边长为2的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论:①MF=MC;②AH⊥EF;③AP2=PMPH; ④EF的最小值是![]() .其中正确的是________.(把你认为正确结论的序号都填上)
.其中正确的是________.(把你认为正确结论的序号都填上)
【答案】②③④
【解析】
①可用特殊值法证明,当![]() 为
为![]() 的中点时,
的中点时,![]() ,可见
,可见![]() .
.
②可连接![]() ,交
,交![]() 于点
于点![]() ,先根据
,先根据![]() 证明
证明![]() ,得到
,得到![]() ,根据矩形的性质可得
,根据矩形的性质可得![]() ,故
,故![]() ,又因为
,又因为![]() ,故
,故![]() ,故
,故![]() .
.
③先证明![]() ,得到
,得到![]() ,再根据
,再根据![]() ,得到
,得到![]() ,代换可得.
,代换可得.
④根据![]() ,可知当
,可知当![]() 取最小值时,
取最小值时,![]() 也取最小值,根据点到直线的距离也就是垂线段最短可得,当
也取最小值,根据点到直线的距离也就是垂线段最短可得,当![]() 时,
时,![]() 取最小值,再通过计算可得.
取最小值,再通过计算可得.
解:
①错误.当![]() 为
为![]() 的中点时,
的中点时,![]() ,可见
,可见![]() ;
;
②正确.
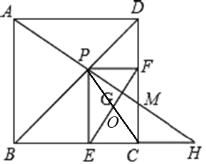
如图,连接![]() ,交
,交![]() 于点
于点![]() ,
,
![]()
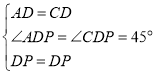
![]()
![]()
![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 为矩形,
为矩形,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
③正确.
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
又![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
④正确.
![]()
![]() 且四边形
且四边形![]() 为矩形,
为矩形,
![]()
![]() ,
,
![]() 当
当![]() 时,
时,![]() 取最小值,
取最小值,
此时![]() ,
,
故![]() 的最小值为
的最小值为![]() .
.
故答案为:②③④.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目