题目内容
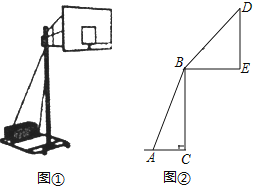
【题目】如图,在△ABC中,O为AC上一点,以点O为圆心,OC为半径做圆,与BC相切于点C,点A作AD⊥BO交BO的延长线于点D,且∠AOD=∠BAD.

(1)求证:AB为⊙O的切线;
(2)若BC=6,tan∠ABC=![]() ,求⊙O的半径和AD的长.
,求⊙O的半径和AD的长.
【答案】(1)见解析;(2)3,![]() .
.
【解析】
(1)作OE⊥AB,先由∠AOD=∠BAD求得∠ABD=∠OAD,再由∠BCO=∠D=90°及∠BOC=∠AOD求得∠OBC=∠OAD=∠ABD,最后证△BOC≌△BOE得OE=OC,依据切线的判定可得;
(2)先求得∠EOA=∠ABC,在Rt△ABC中求得AC=8、AB=10,由切线长定理知BE=BC=6、AE=4、OE=3,继而得BO=3![]() ,再证△ABD∽△OBC,得
,再证△ABD∽△OBC,得![]() ,据此可得答案.
,据此可得答案.
(1)过点O作OE⊥AB于点E,

∵AD⊥BO于点D,
∴∠D=90°,
∴∠BAD+∠ABD=90°,
∠AOD+∠OAD=90°,
∵∠AOD=∠BAD,
∴∠ABD=∠OAD,
又∵BC为⊙O的切线,
∴AC⊥BC,
∴∠BOC=∠D=90°,
∵∠BOC=∠AOD,
∴∠OBC=∠OAD=∠ABD,
∴OE=OC,
∵OE⊥AB,
∴AB是⊙O的切线.
(2)∵∠ABC+∠BAC=90°
∠EOA+∠BAC=90°,
∴∠EOA=∠ABC,
∵tan∠ABC=![]() 、BC=6,
、BC=6,
∴AC=BCtan∠ABC=8,
则AB=10,
由(1)知BE=BC=6,
∴AE=4,
∵tan∠EOA=tan∠ABC=![]() ,
,
∴OE=3,![]() ,
,
∵∠ABD=∠OBC,∠D=∠ACB=90°,
∴△ABD∽△OBC,
∴![]() ,即
,即![]()
∴![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目