题目内容
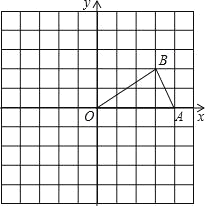
【题目】如图,在直角坐标系中,先描出点![]() ,点
,点![]() .
.
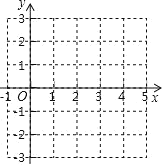
(1)描出点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 的位置,写出
的位置,写出![]() 的坐标 ;
的坐标 ;
(2)用尺规在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小(保留作图痕迹);
的值最小(保留作图痕迹);
(3)用尺规在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() (保留作图痕迹).
(保留作图痕迹).
【答案】(1)(1,-3) (2)答案详见解析 (3)答案详见解析
【解析】
(1)点关于x轴对称,横坐标不变,纵坐标变为相反数;
(2)若要使![]() 的值最小,根据两点之间线段最短原理,可知只需要连接
的值最小,根据两点之间线段最短原理,可知只需要连接![]() 即可,
即可,![]() 与x轴的交点,即为点C.
与x轴的交点,即为点C.
(3)若使![]() ,只需要作出直线AB的垂直平分线即可.
,只需要作出直线AB的垂直平分线即可.
(1)点关于x轴对称,横坐标不变,纵坐标变为相反数,因为![]() ,故A关于x轴的对称点为
,故A关于x轴的对称点为![]() ,
,
(2)根据题意,若要使![]() 的值最小,根据两点之间线段最短原理,可知只需要连接
的值最小,根据两点之间线段最短原理,可知只需要连接![]() 即可,
即可,![]() 与x轴的交点,即为点C,具体作图如下:
与x轴的交点,即为点C,具体作图如下:

(3)若使![]() ,只需要作出直线AB的垂直平分线即可.具体作图如下:
,只需要作出直线AB的垂直平分线即可.具体作图如下:


【题目】李克强总理说:”一个国家养成全民阅读习惯非常重要…我希望全民阅读能够形成一种氛围,无处不在.“为了响应国家的号召,某”希望“学校的全体师生掀起了阅读的热潮.下面是该校三个年级的学生人数分布扇形统计图与学生在4月份阅读课外书籍人次的统计图表,其中七年级的学生人数为240人.请解答下列问题:
图书种类 | 频数 | 频率 |
科普书籍 | A | B |
文学 | 1200 | C |
漫画丛书 | D | 0.35 |
其他 | 200 | 0.05 |
(1)该校七年级学生人数所在扇形的圆心角为______°,该校的学生总人数为______人;
(2)请补全条形统计图;
(3)为了鼓励学生读书,学校决定在“五四”青年节举行两场读书报告会.报告会的内容从“科普书籍”“文学”“漫画丛书”“其他”中任选两个.用画树状图或列表的方法求两场报告会的内容恰好是“科普书籍”与“漫画丛书”的概率.(“科普书籍”“文学”“漫画丛书”“其他”,可以分别用K,W,M,Q来表示)