题目内容
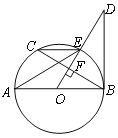
【题目】如图,将等腰直角三角板ABC的直角顶点C放在直线l上,从另两个顶点A、B分别作l的垂线,垂足分别为D、E.
(1)找出图中的全等三角形,并加以证明;
(2)若DE=a,求直角梯形DABE的面积.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据AAS定理证明△ADC≌△CEB;
(2)根据全等三角形的性质得到AD=CE,CD=BE,根据梯形的面积公式计算即可.
解:(1)△ACD≌△CBE,证明如下:
∵△ABC是等腰直角三角形,C为直角顶点,∴AC=CB
∵AD⊥l,BE⊥l,∴∠ADC=∠CEB=90°
在Rt△ACD中,∠DAC+∠DCA=90°
∵∠ACB=900,∴∠ECB+∠DCA=90°,
∴∠DAC=∠ECB
在△ACD和△CBE中,
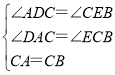
∴△ACD≌△CBE
(2)由(1)知,△ACD≌△CBE,∴AD=CE,CD=BE
∴AD+BE=CE+CD=DE=a,
∴直角梯形DABE的面积=![]() ×(AD+BE)×DE=
×(AD+BE)×DE=![]() .
.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目